| L(s) = 1 | − 2·2-s + 4-s + 2·5-s + 2·8-s − 4·10-s − 4·16-s − 2·19-s + 2·20-s − 2·23-s + 25-s + 2·32-s + 4·38-s + 4·40-s + 4·46-s + 2·47-s − 2·49-s − 2·50-s + 2·53-s + 3·64-s − 2·76-s − 8·80-s − 2·92-s − 4·94-s − 4·95-s + 4·98-s + 100-s − 4·106-s + ⋯ |
| L(s) = 1 | − 2·2-s + 4-s + 2·5-s + 2·8-s − 4·10-s − 4·16-s − 2·19-s + 2·20-s − 2·23-s + 25-s + 2·32-s + 4·38-s + 4·40-s + 4·46-s + 2·47-s − 2·49-s − 2·50-s + 2·53-s + 3·64-s − 2·76-s − 8·80-s − 2·92-s − 4·94-s − 4·95-s + 4·98-s + 100-s − 4·106-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{12} \cdot 3^{8} \cdot 5^{4} \cdot 7^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{12} \cdot 3^{8} \cdot 5^{4} \cdot 7^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(\frac{1}{2})\) |
\(\approx\) |
\(0.5029531838\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.5029531838\) |
| \(L(1)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_2$ | \( ( 1 + T + T^{2} )^{2} \) |
| 3 | | \( 1 \) |
| 5 | $C_2$ | \( ( 1 - T + T^{2} )^{2} \) |
| 7 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| good | 11 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 13 | $C_2^2$ | \( ( 1 - T^{2} + T^{4} )^{2} \) |
| 17 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 19 | $C_1$$\times$$C_2$ | \( ( 1 + T )^{4}( 1 - T + T^{2} )^{2} \) |
| 23 | $C_1$$\times$$C_2$ | \( ( 1 + T )^{4}( 1 - T + T^{2} )^{2} \) |
| 29 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 31 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 37 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 41 | $C_2^2$ | \( ( 1 - T^{2} + T^{4} )^{2} \) |
| 43 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 47 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{4}( 1 + T + T^{2} )^{2} \) |
| 53 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{4}( 1 + T + T^{2} )^{2} \) |
| 59 | $C_2^2$ | \( ( 1 - T^{2} + T^{4} )^{2} \) |
| 61 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 67 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 71 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 73 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 79 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 83 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 89 | $C_2^2$ | \( ( 1 - T^{2} + T^{4} )^{2} \) |
| 97 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
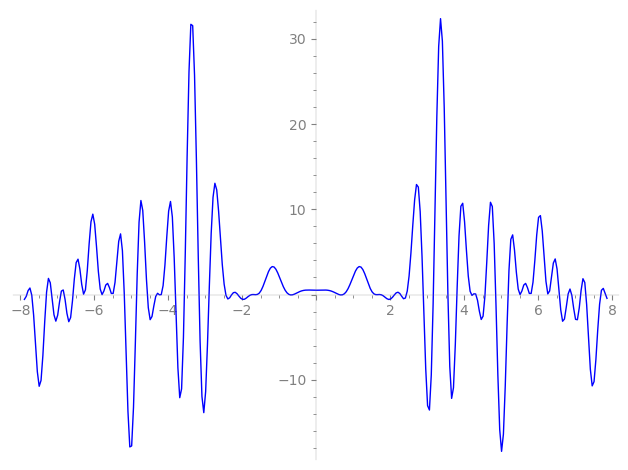
Imaginary part of the first few zeros on the critical line
−6.57353155962901573915586939451, −6.28154495251464900403373981457, −6.27115650833818183539131750822, −5.79523984363789229939104948339, −5.78077217044983124208164598929, −5.51940522887001682602665338057, −5.50491354071707484736288524031, −5.18752993853505047890348709297, −4.85365279820322811340395280069, −4.56466019230544709108542002929, −4.31932665036546984463636217158, −4.24537433939005443392608169263, −4.18678632794795845858004239453, −3.80522931322031377883077033047, −3.56123711740943228490597015783, −3.16709552451382687345996459902, −2.89541896766017436989623744916, −2.44368414825167346409632343769, −2.28155376534316570216692694291, −2.12153986388494405744184416180, −1.71264965498424671970413934753, −1.70773828801080606897512908778, −1.59596008749811061438707404629, −0.73153284600720958533665269965, −0.61257256774891144671805280039,
0.61257256774891144671805280039, 0.73153284600720958533665269965, 1.59596008749811061438707404629, 1.70773828801080606897512908778, 1.71264965498424671970413934753, 2.12153986388494405744184416180, 2.28155376534316570216692694291, 2.44368414825167346409632343769, 2.89541896766017436989623744916, 3.16709552451382687345996459902, 3.56123711740943228490597015783, 3.80522931322031377883077033047, 4.18678632794795845858004239453, 4.24537433939005443392608169263, 4.31932665036546984463636217158, 4.56466019230544709108542002929, 4.85365279820322811340395280069, 5.18752993853505047890348709297, 5.50491354071707484736288524031, 5.51940522887001682602665338057, 5.78077217044983124208164598929, 5.79523984363789229939104948339, 6.27115650833818183539131750822, 6.28154495251464900403373981457, 6.57353155962901573915586939451