| L(s) = 1 | + (−0.866 − 0.5i)2-s + (1.66 − 0.464i)3-s + (0.499 + 0.866i)4-s + (−0.5 + 0.866i)5-s + (−1.67 − 0.431i)6-s + (−0.311 − 2.62i)7-s − 0.999i·8-s + (2.56 − 1.55i)9-s + (0.866 − 0.499i)10-s + (4.44 − 2.56i)11-s + (1.23 + 1.21i)12-s + 5.00i·13-s + (−1.04 + 2.43i)14-s + (−0.431 + 1.67i)15-s + (−0.5 + 0.866i)16-s + (−1.87 − 3.25i)17-s + ⋯ |
| L(s) = 1 | + (−0.612 − 0.353i)2-s + (0.963 − 0.268i)3-s + (0.249 + 0.433i)4-s + (−0.223 + 0.387i)5-s + (−0.684 − 0.176i)6-s + (−0.117 − 0.993i)7-s − 0.353i·8-s + (0.855 − 0.517i)9-s + (0.273 − 0.158i)10-s + (1.34 − 0.774i)11-s + (0.357 + 0.350i)12-s + 1.38i·13-s + (−0.279 + 0.649i)14-s + (−0.111 + 0.433i)15-s + (−0.125 + 0.216i)16-s + (−0.455 − 0.789i)17-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 210 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.707 + 0.706i)\, \overline{\Lambda}(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 210 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.707 + 0.706i)\, \overline{\Lambda}(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(1.13691 - 0.470160i\) |
| \(L(\frac12)\) |
\(\approx\) |
\(1.13691 - 0.470160i\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ |
|---|
| bad | 2 | \( 1 + (0.866 + 0.5i)T \) |
| 3 | \( 1 + (-1.66 + 0.464i)T \) |
| 5 | \( 1 + (0.5 - 0.866i)T \) |
| 7 | \( 1 + (0.311 + 2.62i)T \) |
| good | 11 | \( 1 + (-4.44 + 2.56i)T + (5.5 - 9.52i)T^{2} \) |
| 13 | \( 1 - 5.00iT - 13T^{2} \) |
| 17 | \( 1 + (1.87 + 3.25i)T + (-8.5 + 14.7i)T^{2} \) |
| 19 | \( 1 + (-2.33 - 1.34i)T + (9.5 + 16.4i)T^{2} \) |
| 23 | \( 1 + (2.15 + 1.24i)T + (11.5 + 19.9i)T^{2} \) |
| 29 | \( 1 - 6.18iT - 29T^{2} \) |
| 31 | \( 1 + (4.13 - 2.38i)T + (15.5 - 26.8i)T^{2} \) |
| 37 | \( 1 + (0.0262 - 0.0453i)T + (-18.5 - 32.0i)T^{2} \) |
| 41 | \( 1 + 6.55T + 41T^{2} \) |
| 43 | \( 1 + 9.45T + 43T^{2} \) |
| 47 | \( 1 + (1.53 - 2.65i)T + (-23.5 - 40.7i)T^{2} \) |
| 53 | \( 1 + (-0.963 + 0.556i)T + (26.5 - 45.8i)T^{2} \) |
| 59 | \( 1 + (-6.63 - 11.4i)T + (-29.5 + 51.0i)T^{2} \) |
| 61 | \( 1 + (-3.59 - 2.07i)T + (30.5 + 52.8i)T^{2} \) |
| 67 | \( 1 + (-0.448 - 0.776i)T + (-33.5 + 58.0i)T^{2} \) |
| 71 | \( 1 - 13.4iT - 71T^{2} \) |
| 73 | \( 1 + (6.04 - 3.49i)T + (36.5 - 63.2i)T^{2} \) |
| 79 | \( 1 + (-8.37 + 14.5i)T + (-39.5 - 68.4i)T^{2} \) |
| 83 | \( 1 - 1.37T + 83T^{2} \) |
| 89 | \( 1 + (2.67 - 4.62i)T + (-44.5 - 77.0i)T^{2} \) |
| 97 | \( 1 + 0.633iT - 97T^{2} \) |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
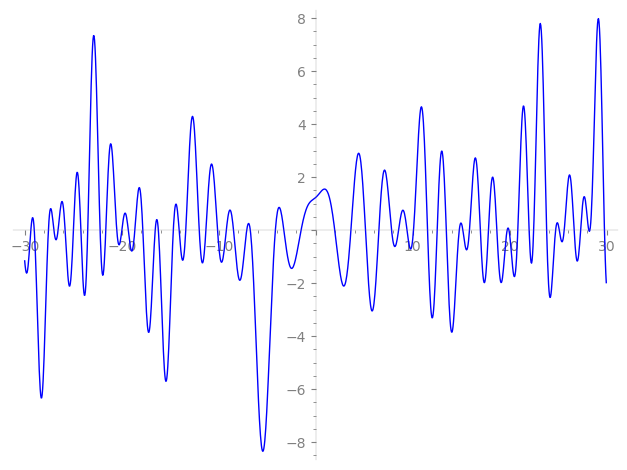
Imaginary part of the first few zeros on the critical line
−12.00766203386490357101932722164, −11.31876264531476701050319879157, −10.12240467222713444485660287731, −9.214687530190502687987362357639, −8.475471817001115763954224975846, −7.11011534053308698551576312500, −6.74635298132675352046698621086, −4.15863294066273862800591243948, −3.28681677357024742275500960090, −1.50587707605282386164723229333,
1.95837115231024889127422958033, 3.62980542182048630257313955960, 5.12746563558592499879797477390, 6.50965113409706063336637651648, 7.81482987671661410664017530017, 8.543640572257935527896785465603, 9.408574266974598019254934585610, 10.08009952900484034098634086123, 11.52352961192705591601298613760, 12.51799285114596992398198013491