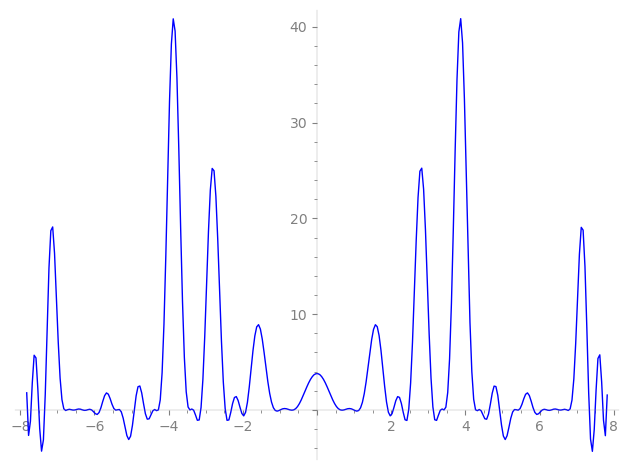
| L(s) = 1 | − 4·3-s + 4·5-s − 4·7-s + 10·9-s + 2·11-s + 2·13-s − 16·15-s + 2·17-s + 16·21-s − 2·23-s + 10·25-s − 20·27-s + 20·29-s + 4·31-s − 8·33-s − 16·35-s + 4·37-s − 8·39-s + 6·41-s − 2·43-s + 40·45-s + 2·47-s + 8·49-s − 8·51-s − 6·53-s + 8·55-s + 8·61-s + ⋯ |
| L(s) = 1 | − 2.30·3-s + 1.78·5-s − 1.51·7-s + 10/3·9-s + 0.603·11-s + 0.554·13-s − 4.13·15-s + 0.485·17-s + 3.49·21-s − 0.417·23-s + 2·25-s − 3.84·27-s + 3.71·29-s + 0.718·31-s − 1.39·33-s − 2.70·35-s + 0.657·37-s − 1.28·39-s + 0.937·41-s − 0.304·43-s + 5.96·45-s + 0.291·47-s + 8/7·49-s − 1.12·51-s − 0.824·53-s + 1.07·55-s + 1.02·61-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{8} \cdot 3^{4} \cdot 5^{4} \cdot 31^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(2-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{8} \cdot 3^{4} \cdot 5^{4} \cdot 31^{4}\right)^{s/2} \, \Gamma_{\C}(s+1/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(3.805314303\) |
| \(L(\frac12)\) |
\(\approx\) |
\(3.805314303\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | | \( 1 \) |
| 3 | $C_1$ | \( ( 1 + T )^{4} \) |
| 5 | $C_1$ | \( ( 1 - T )^{4} \) |
| 31 | $C_1$ | \( ( 1 - T )^{4} \) |
| good | 7 | $C_2 \wr S_4$ | \( 1 + 4 T + 8 T^{2} + 30 T^{3} + 130 T^{4} + 30 p T^{5} + 8 p^{2} T^{6} + 4 p^{3} T^{7} + p^{4} T^{8} \) |
| 11 | $C_2 \wr S_4$ | \( 1 - 2 T + 6 T^{3} - 18 T^{4} + 6 p T^{5} - 2 p^{3} T^{7} + p^{4} T^{8} \) |
| 13 | $C_2 \wr S_4$ | \( 1 - 2 T + 16 T^{2} + 4 T^{3} + 166 T^{4} + 4 p T^{5} + 16 p^{2} T^{6} - 2 p^{3} T^{7} + p^{4} T^{8} \) |
| 17 | $C_2 \wr S_4$ | \( 1 - 2 T + 28 T^{2} + 6 T^{3} + 470 T^{4} + 6 p T^{5} + 28 p^{2} T^{6} - 2 p^{3} T^{7} + p^{4} T^{8} \) |
| 19 | $C_2$ | \( ( 1 + p T^{2} )^{4} \) |
| 23 | $C_2 \wr S_4$ | \( 1 + 2 T + 52 T^{2} + 30 T^{3} + 1430 T^{4} + 30 p T^{5} + 52 p^{2} T^{6} + 2 p^{3} T^{7} + p^{4} T^{8} \) |
| 29 | $C_2 \wr S_4$ | \( 1 - 20 T + 214 T^{2} - 1526 T^{3} + 8886 T^{4} - 1526 p T^{5} + 214 p^{2} T^{6} - 20 p^{3} T^{7} + p^{4} T^{8} \) |
| 37 | $C_2 \wr S_4$ | \( 1 - 4 T + 128 T^{2} - 402 T^{3} + 6862 T^{4} - 402 p T^{5} + 128 p^{2} T^{6} - 4 p^{3} T^{7} + p^{4} T^{8} \) |
| 41 | $C_2 \wr S_4$ | \( 1 - 6 T + 132 T^{2} - 642 T^{3} + 7654 T^{4} - 642 p T^{5} + 132 p^{2} T^{6} - 6 p^{3} T^{7} + p^{4} T^{8} \) |
| 43 | $C_2 \wr S_4$ | \( 1 + 2 T + 128 T^{2} + 186 T^{3} + 7534 T^{4} + 186 p T^{5} + 128 p^{2} T^{6} + 2 p^{3} T^{7} + p^{4} T^{8} \) |
| 47 | $C_2 \wr S_4$ | \( 1 - 2 T + 76 T^{2} - 270 T^{3} + 2798 T^{4} - 270 p T^{5} + 76 p^{2} T^{6} - 2 p^{3} T^{7} + p^{4} T^{8} \) |
| 53 | $C_2 \wr S_4$ | \( 1 + 6 T + 112 T^{2} + 526 T^{3} + 5902 T^{4} + 526 p T^{5} + 112 p^{2} T^{6} + 6 p^{3} T^{7} + p^{4} T^{8} \) |
| 59 | $C_2 \wr S_4$ | \( 1 - 66 T^{2} + 54 T^{3} + 7066 T^{4} + 54 p T^{5} - 66 p^{2} T^{6} + p^{4} T^{8} \) |
| 61 | $C_2 \wr S_4$ | \( 1 - 8 T + 92 T^{2} - 504 T^{3} + 2774 T^{4} - 504 p T^{5} + 92 p^{2} T^{6} - 8 p^{3} T^{7} + p^{4} T^{8} \) |
| 67 | $C_2 \wr S_4$ | \( 1 - 10 T + 152 T^{2} - 1632 T^{3} + 14306 T^{4} - 1632 p T^{5} + 152 p^{2} T^{6} - 10 p^{3} T^{7} + p^{4} T^{8} \) |
| 71 | $C_2 \wr S_4$ | \( 1 - 2 T + 234 T^{2} - 300 T^{3} + 23290 T^{4} - 300 p T^{5} + 234 p^{2} T^{6} - 2 p^{3} T^{7} + p^{4} T^{8} \) |
| 73 | $C_2 \wr S_4$ | \( 1 - 16 T + 248 T^{2} - 2634 T^{3} + 28006 T^{4} - 2634 p T^{5} + 248 p^{2} T^{6} - 16 p^{3} T^{7} + p^{4} T^{8} \) |
| 79 | $C_2 \wr S_4$ | \( 1 - 20 T + 332 T^{2} - 3096 T^{3} + 31910 T^{4} - 3096 p T^{5} + 332 p^{2} T^{6} - 20 p^{3} T^{7} + p^{4} T^{8} \) |
| 83 | $C_2 \wr S_4$ | \( 1 + 14 T + 364 T^{2} + 3434 T^{3} + 46662 T^{4} + 3434 p T^{5} + 364 p^{2} T^{6} + 14 p^{3} T^{7} + p^{4} T^{8} \) |
| 89 | $C_2 \wr S_4$ | \( 1 - 26 T + 558 T^{2} - 7296 T^{3} + 82798 T^{4} - 7296 p T^{5} + 558 p^{2} T^{6} - 26 p^{3} T^{7} + p^{4} T^{8} \) |
| 97 | $C_2 \wr S_4$ | \( 1 - 14 T + 164 T^{2} + 150 T^{3} - 3130 T^{4} + 150 p T^{5} + 164 p^{2} T^{6} - 14 p^{3} T^{7} + p^{4} T^{8} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−6.52144176354639406509458549930, −6.32042690351850996422216440465, −6.19612395598375788745882784606, −6.07525159723471227427122589370, −5.84507202004384494308870133171, −5.44190602469552744593154809381, −5.38706574415063829061376240872, −5.30833943616629969371929517164, −4.92451154106650328407147519166, −4.64704121024132259703949796097, −4.40739500982061174724552559875, −4.35133592239639819165606827107, −4.27597904743668398719259532316, −3.43299273482973327892985230932, −3.42445623405953880804460978722, −3.32987668560981668989224962809, −3.13203359390914837788505047810, −2.47207354877037958000623517993, −2.31152238182531616578522389529, −2.05636984556339213219108150791, −1.91022400832669488510696850939, −1.13971253702006093138842904092, −0.991617232010597417022895363155, −0.72453388706747848813545719913, −0.63128021278243154715269417238,
0.63128021278243154715269417238, 0.72453388706747848813545719913, 0.991617232010597417022895363155, 1.13971253702006093138842904092, 1.91022400832669488510696850939, 2.05636984556339213219108150791, 2.31152238182531616578522389529, 2.47207354877037958000623517993, 3.13203359390914837788505047810, 3.32987668560981668989224962809, 3.42445623405953880804460978722, 3.43299273482973327892985230932, 4.27597904743668398719259532316, 4.35133592239639819165606827107, 4.40739500982061174724552559875, 4.64704121024132259703949796097, 4.92451154106650328407147519166, 5.30833943616629969371929517164, 5.38706574415063829061376240872, 5.44190602469552744593154809381, 5.84507202004384494308870133171, 6.07525159723471227427122589370, 6.19612395598375788745882784606, 6.32042690351850996422216440465, 6.52144176354639406509458549930