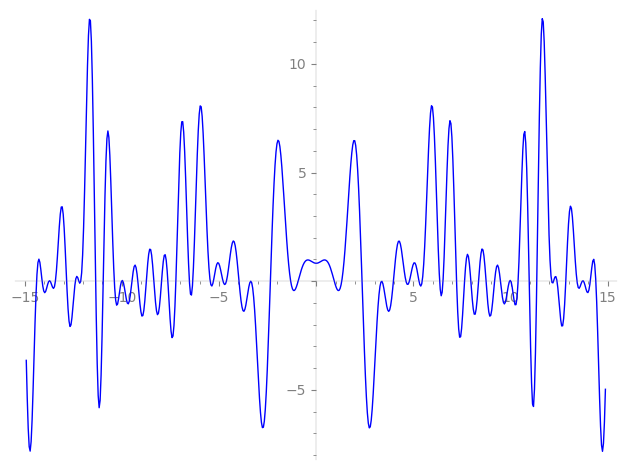
| L(s) = 1 | − 2·4-s + 9-s + 3·16-s + 2·19-s + 2·29-s − 2·36-s − 2·41-s + 49-s − 2·59-s − 4·64-s + 4·71-s − 4·76-s + 2·79-s − 4·116-s + 2·121-s + 127-s + 131-s + 137-s + 139-s + 3·144-s + 149-s + 151-s + 157-s + 163-s + 4·164-s + 167-s − 2·169-s + ⋯ |
| L(s) = 1 | − 2·4-s + 9-s + 3·16-s + 2·19-s + 2·29-s − 2·36-s − 2·41-s + 49-s − 2·59-s − 4·64-s + 4·71-s − 4·76-s + 2·79-s − 4·116-s + 2·121-s + 127-s + 131-s + 137-s + 139-s + 3·144-s + 149-s + 151-s + 157-s + 163-s + 4·164-s + 167-s − 2·169-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 2175625 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 2175625 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(\frac{1}{2})\) |
\(\approx\) |
\(0.8246668873\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.8246668873\) |
| \(L(1)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 5 | | \( 1 \) |
| 59 | $C_1$ | \( ( 1 + T )^{2} \) |
| good | 2 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| 3 | $C_2^2$ | \( 1 - T^{2} + T^{4} \) |
| 7 | $C_2^2$ | \( 1 - T^{2} + T^{4} \) |
| 11 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{2}( 1 + T )^{2} \) |
| 13 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| 17 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| 19 | $C_2$ | \( ( 1 - T + T^{2} )^{2} \) |
| 23 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| 29 | $C_2$ | \( ( 1 - T + T^{2} )^{2} \) |
| 31 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{2}( 1 + T )^{2} \) |
| 37 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| 41 | $C_2$ | \( ( 1 + T + T^{2} )^{2} \) |
| 43 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| 47 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| 53 | $C_2^2$ | \( 1 - T^{2} + T^{4} \) |
| 61 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{2}( 1 + T )^{2} \) |
| 67 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| 71 | $C_1$ | \( ( 1 - T )^{4} \) |
| 73 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| 79 | $C_2$ | \( ( 1 - T + T^{2} )^{2} \) |
| 83 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| 89 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{2}( 1 + T )^{2} \) |
| 97 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−9.945826660555327794197667741707, −9.480129619530206138576788579576, −9.178777683657520965747773266920, −8.740500216264505303932462431537, −8.353602308357405452278563195226, −7.956948618646354368416497079220, −7.63347650989305275420538295227, −7.22132896509127137856520811057, −6.52453096764973979675555908017, −6.35304892711875341882813006434, −5.45405101313080788572919415799, −5.29047218150297243434544037814, −4.79332800926440087125155738542, −4.61994960548872640396167089395, −3.97217197845135319073125238752, −3.36794109633057234360602774170, −3.36457973803491779224947195532, −2.35822295102411041191841247252, −1.31362682131113756051108051552, −0.930032885137165132047674498048,
0.930032885137165132047674498048, 1.31362682131113756051108051552, 2.35822295102411041191841247252, 3.36457973803491779224947195532, 3.36794109633057234360602774170, 3.97217197845135319073125238752, 4.61994960548872640396167089395, 4.79332800926440087125155738542, 5.29047218150297243434544037814, 5.45405101313080788572919415799, 6.35304892711875341882813006434, 6.52453096764973979675555908017, 7.22132896509127137856520811057, 7.63347650989305275420538295227, 7.956948618646354368416497079220, 8.353602308357405452278563195226, 8.740500216264505303932462431537, 9.178777683657520965747773266920, 9.480129619530206138576788579576, 9.945826660555327794197667741707