| L(s) = 1 | + 4·4-s − 6·5-s + 12·16-s − 24·20-s + 19·25-s − 20·31-s + 10·49-s + 12·53-s + 32·64-s − 40·79-s − 72·80-s + 60·83-s + 76·100-s − 60·107-s − 10·121-s − 80·124-s − 42·125-s + 127-s + 131-s + 137-s + 139-s + 149-s + 151-s + 120·155-s + 157-s + 163-s + 167-s + ⋯ |
| L(s) = 1 | + 2·4-s − 2.68·5-s + 3·16-s − 5.36·20-s + 19/5·25-s − 3.59·31-s + 10/7·49-s + 1.64·53-s + 4·64-s − 4.50·79-s − 8.04·80-s + 6.58·83-s + 38/5·100-s − 5.80·107-s − 0.909·121-s − 7.18·124-s − 3.75·125-s + 0.0887·127-s + 0.0873·131-s + 0.0854·137-s + 0.0848·139-s + 0.0819·149-s + 0.0813·151-s + 9.63·155-s + 0.0798·157-s + 0.0783·163-s + 0.0773·167-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{12} \cdot 3^{12} \cdot 5^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(2-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{12} \cdot 3^{12} \cdot 5^{4}\right)^{s/2} \, \Gamma_{\C}(s+1/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(1.106099075\) |
| \(L(\frac12)\) |
\(\approx\) |
\(1.106099075\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_2$ | \( ( 1 - p T^{2} )^{2} \) |
| 3 | | \( 1 \) |
| 5 | $C_2^2$ | \( 1 + 6 T + 17 T^{2} + 6 p T^{3} + p^{2} T^{4} \) |
| good | 7 | $C_2^2$$\times$$C_2^2$ | \( ( 1 - 2 T - 3 T^{2} - 2 p T^{3} + p^{2} T^{4} )( 1 + 2 T - 3 T^{2} + 2 p T^{3} + p^{2} T^{4} ) \) |
| 11 | $C_2^2$$\times$$C_2^2$ | \( ( 1 - 6 T + 23 T^{2} - 6 p T^{3} + p^{2} T^{4} )( 1 + 6 T + 23 T^{2} + 6 p T^{3} + p^{2} T^{4} ) \) |
| 13 | $C_2$ | \( ( 1 + p T^{2} )^{4} \) |
| 17 | $C_2$ | \( ( 1 - p T^{2} )^{4} \) |
| 19 | $C_2$ | \( ( 1 - p T^{2} )^{4} \) |
| 23 | $C_2$ | \( ( 1 - p T^{2} )^{4} \) |
| 29 | $C_2^2$ | \( ( 1 + 50 T^{2} + p^{2} T^{4} )^{2} \) |
| 31 | $C_2^2$ | \( ( 1 + 10 T + 69 T^{2} + 10 p T^{3} + p^{2} T^{4} )^{2} \) |
| 37 | $C_2$ | \( ( 1 + p T^{2} )^{4} \) |
| 41 | $C_2$ | \( ( 1 + p T^{2} )^{4} \) |
| 43 | $C_2$ | \( ( 1 + p T^{2} )^{4} \) |
| 47 | $C_2$ | \( ( 1 - p T^{2} )^{4} \) |
| 53 | $C_2^2$ | \( ( 1 - 6 T + 65 T^{2} - 6 p T^{3} + p^{2} T^{4} )^{2} \) |
| 59 | $C_2^2$ | \( ( 1 - 10 T^{2} + p^{2} T^{4} )^{2} \) |
| 61 | $C_2$ | \( ( 1 - p T^{2} )^{4} \) |
| 67 | $C_2$ | \( ( 1 + p T^{2} )^{4} \) |
| 71 | $C_2$ | \( ( 1 + p T^{2} )^{4} \) |
| 73 | $C_2^2$$\times$$C_2^2$ | \( ( 1 - 14 T + 123 T^{2} - 14 p T^{3} + p^{2} T^{4} )( 1 + 14 T + 123 T^{2} + 14 p T^{3} + p^{2} T^{4} ) \) |
| 79 | $C_2$ | \( ( 1 + 10 T + p T^{2} )^{4} \) |
| 83 | $C_2^2$ | \( ( 1 - 30 T + 383 T^{2} - 30 p T^{3} + p^{2} T^{4} )^{2} \) |
| 89 | $C_2$ | \( ( 1 + p T^{2} )^{4} \) |
| 97 | $C_2^2$$\times$$C_2^2$ | \( ( 1 - 2 T - 93 T^{2} - 2 p T^{3} + p^{2} T^{4} )( 1 + 2 T - 93 T^{2} + 2 p T^{3} + p^{2} T^{4} ) \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
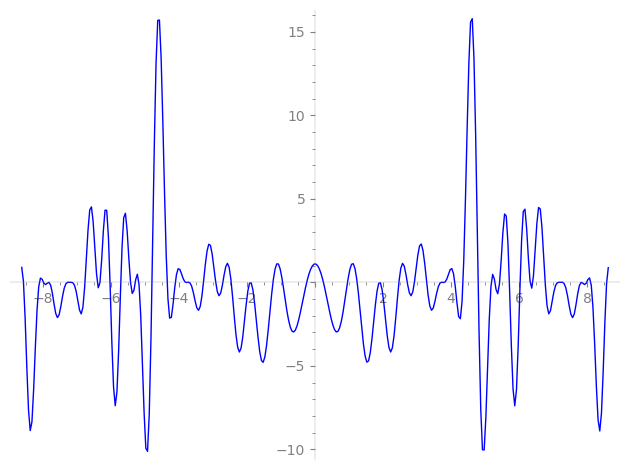
Imaginary part of the first few zeros on the critical line
−7.18928437221459298800737633874, −7.16535593264321197275013763858, −6.76709491719538137023362591994, −6.40448213947791435199835599394, −6.32607000922799236867862476661, −6.03049482267964768227148087819, −5.71389288753232826704802898649, −5.42711927250927920450498141208, −5.28868054203616181863375573761, −5.18293250058691254532416117428, −4.79667600347633090632351756607, −4.34957476433615146161598515773, −4.10883867078555291366045872310, −3.81121222313899292083872701241, −3.74574349041979696193622002586, −3.70032483657566103174624675519, −3.28226070061942599080706182488, −2.92118570596860189924075230221, −2.71142900043232155945759440648, −2.46633477721850670044807430316, −1.91370239420974618138306191590, −1.88698072817727331270433788293, −1.23768096791501890639054922918, −0.954180474857727631308630951056, −0.24552557685604355251344144376,
0.24552557685604355251344144376, 0.954180474857727631308630951056, 1.23768096791501890639054922918, 1.88698072817727331270433788293, 1.91370239420974618138306191590, 2.46633477721850670044807430316, 2.71142900043232155945759440648, 2.92118570596860189924075230221, 3.28226070061942599080706182488, 3.70032483657566103174624675519, 3.74574349041979696193622002586, 3.81121222313899292083872701241, 4.10883867078555291366045872310, 4.34957476433615146161598515773, 4.79667600347633090632351756607, 5.18293250058691254532416117428, 5.28868054203616181863375573761, 5.42711927250927920450498141208, 5.71389288753232826704802898649, 6.03049482267964768227148087819, 6.32607000922799236867862476661, 6.40448213947791435199835599394, 6.76709491719538137023362591994, 7.16535593264321197275013763858, 7.18928437221459298800737633874