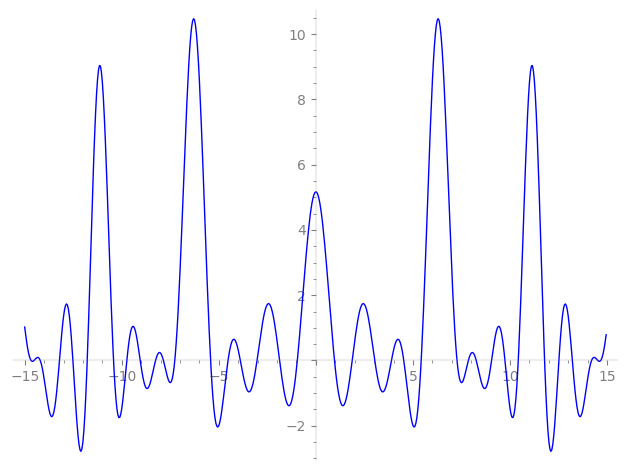
| L(s) = 1 | + 0.506·2-s + 30.1·3-s − 31.7·4-s − 25·5-s + 15.2·6-s + 184.·7-s − 32.2·8-s + 664.·9-s − 12.6·10-s + 121·11-s − 956.·12-s − 525.·13-s + 93.5·14-s − 752.·15-s + 999.·16-s + 2.23e3·17-s + 336.·18-s − 361·19-s + 793.·20-s + 5.56e3·21-s + 61.3·22-s − 728.·23-s − 972.·24-s + 625·25-s − 266.·26-s + 1.26e4·27-s − 5.86e3·28-s + ⋯ |
| L(s) = 1 | + 0.0895·2-s + 1.93·3-s − 0.991·4-s − 0.447·5-s + 0.173·6-s + 1.42·7-s − 0.178·8-s + 2.73·9-s − 0.0400·10-s + 0.301·11-s − 1.91·12-s − 0.863·13-s + 0.127·14-s − 0.864·15-s + 0.975·16-s + 1.87·17-s + 0.244·18-s − 0.229·19-s + 0.443·20-s + 2.75·21-s + 0.0270·22-s − 0.286·23-s − 0.344·24-s + 0.200·25-s − 0.0773·26-s + 3.34·27-s − 1.41·28-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 1045 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \Lambda(6-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 1045 ^{s/2} \, \Gamma_{\C}(s+5/2) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(3)\) |
\(\approx\) |
\(5.168663260\) |
| \(L(\frac12)\) |
\(\approx\) |
\(5.168663260\) |
| \(L(\frac{7}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ |
|---|
| bad | 5 | \( 1 + 25T \) |
| 11 | \( 1 - 121T \) |
| 19 | \( 1 + 361T \) |
| good | 2 | \( 1 - 0.506T + 32T^{2} \) |
| 3 | \( 1 - 30.1T + 243T^{2} \) |
| 7 | \( 1 - 184.T + 1.68e4T^{2} \) |
| 13 | \( 1 + 525.T + 3.71e5T^{2} \) |
| 17 | \( 1 - 2.23e3T + 1.41e6T^{2} \) |
| 23 | \( 1 + 728.T + 6.43e6T^{2} \) |
| 29 | \( 1 + 2.18e3T + 2.05e7T^{2} \) |
| 31 | \( 1 + 988.T + 2.86e7T^{2} \) |
| 37 | \( 1 + 1.12e3T + 6.93e7T^{2} \) |
| 41 | \( 1 - 9.58e3T + 1.15e8T^{2} \) |
| 43 | \( 1 - 1.67e3T + 1.47e8T^{2} \) |
| 47 | \( 1 + 4.56e3T + 2.29e8T^{2} \) |
| 53 | \( 1 - 3.17e3T + 4.18e8T^{2} \) |
| 59 | \( 1 - 1.16e4T + 7.14e8T^{2} \) |
| 61 | \( 1 - 2.43e4T + 8.44e8T^{2} \) |
| 67 | \( 1 + 2.96e4T + 1.35e9T^{2} \) |
| 71 | \( 1 - 3.37e4T + 1.80e9T^{2} \) |
| 73 | \( 1 - 1.31e3T + 2.07e9T^{2} \) |
| 79 | \( 1 + 5.91e4T + 3.07e9T^{2} \) |
| 83 | \( 1 + 8.99e4T + 3.93e9T^{2} \) |
| 89 | \( 1 - 4.83e4T + 5.58e9T^{2} \) |
| 97 | \( 1 - 1.59e5T + 8.58e9T^{2} \) |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−9.048937410776478226191209262418, −8.258627711280838585722527947487, −7.85298397930862612637873372129, −7.26886949262874928369270695443, −5.42312999378956366608567076170, −4.52597373005498406962072039005, −3.89220246859633211942835287072, −3.03239088416096081167524932819, −1.86945819719230403523177703684, −0.957230923497443159097038522731,
0.957230923497443159097038522731, 1.86945819719230403523177703684, 3.03239088416096081167524932819, 3.89220246859633211942835287072, 4.52597373005498406962072039005, 5.42312999378956366608567076170, 7.26886949262874928369270695443, 7.85298397930862612637873372129, 8.258627711280838585722527947487, 9.048937410776478226191209262418