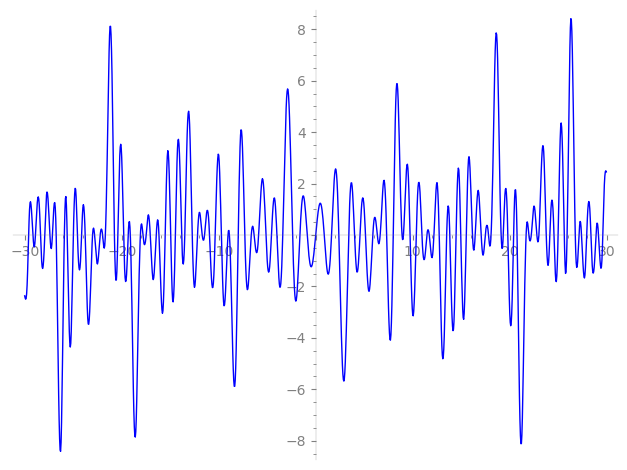
| L(s) = 1 | − 2·3-s + 9-s + 6·11-s − 6·17-s + 2·19-s − 5·25-s + 4·27-s − 12·33-s − 6·41-s + 10·43-s − 7·49-s + 12·51-s − 4·57-s + 6·59-s − 14·67-s + 2·73-s + 10·75-s − 11·81-s + 18·83-s + 18·89-s − 10·97-s + 6·99-s + 101-s + 103-s + 107-s + 109-s + 113-s + ⋯ |
| L(s) = 1 | − 1.15·3-s + 1/3·9-s + 1.80·11-s − 1.45·17-s + 0.458·19-s − 25-s + 0.769·27-s − 2.08·33-s − 0.937·41-s + 1.52·43-s − 49-s + 1.68·51-s − 0.529·57-s + 0.781·59-s − 1.71·67-s + 0.234·73-s + 1.15·75-s − 1.22·81-s + 1.97·83-s + 1.90·89-s − 1.01·97-s + 0.603·99-s + 0.0995·101-s + 0.0985·103-s + 0.0966·107-s + 0.0957·109-s + 0.0940·113-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 43264 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 43264 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 2 | \( 1 \) | |
| 13 | \( 1 \) | |
| good | 3 | \( 1 + 2 T + p T^{2} \) | 1.3.c |
| 5 | \( 1 + p T^{2} \) | 1.5.a |
| 7 | \( 1 + p T^{2} \) | 1.7.a |
| 11 | \( 1 - 6 T + p T^{2} \) | 1.11.ag |
| 17 | \( 1 + 6 T + p T^{2} \) | 1.17.g |
| 19 | \( 1 - 2 T + p T^{2} \) | 1.19.ac |
| 23 | \( 1 + p T^{2} \) | 1.23.a |
| 29 | \( 1 + p T^{2} \) | 1.29.a |
| 31 | \( 1 + p T^{2} \) | 1.31.a |
| 37 | \( 1 + p T^{2} \) | 1.37.a |
| 41 | \( 1 + 6 T + p T^{2} \) | 1.41.g |
| 43 | \( 1 - 10 T + p T^{2} \) | 1.43.ak |
| 47 | \( 1 + p T^{2} \) | 1.47.a |
| 53 | \( 1 + p T^{2} \) | 1.53.a |
| 59 | \( 1 - 6 T + p T^{2} \) | 1.59.ag |
| 61 | \( 1 + p T^{2} \) | 1.61.a |
| 67 | \( 1 + 14 T + p T^{2} \) | 1.67.o |
| 71 | \( 1 + p T^{2} \) | 1.71.a |
| 73 | \( 1 - 2 T + p T^{2} \) | 1.73.ac |
| 79 | \( 1 + p T^{2} \) | 1.79.a |
| 83 | \( 1 - 18 T + p T^{2} \) | 1.83.as |
| 89 | \( 1 - 18 T + p T^{2} \) | 1.89.as |
| 97 | \( 1 + 10 T + p T^{2} \) | 1.97.k |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−14.95134465544795, −14.46623890855581, −13.82104131827494, −13.49676938325751, −12.73072197054595, −12.18891049595484, −11.70710125745063, −11.46059121971409, −10.94724501508226, −10.36367586454735, −9.724501713117323, −9.042566032483952, −8.891792409334331, −7.989740320921697, −7.312452078698935, −6.648781068055916, −6.348488590138742, −5.884767412162913, −5.128616949127503, −4.562617697510791, −3.999966004791063, −3.397774512605483, −2.385974869475617, −1.630933153681201, −0.8783664248622073, 0,
0.8783664248622073, 1.630933153681201, 2.385974869475617, 3.397774512605483, 3.999966004791063, 4.562617697510791, 5.128616949127503, 5.884767412162913, 6.348488590138742, 6.648781068055916, 7.312452078698935, 7.989740320921697, 8.891792409334331, 9.042566032483952, 9.724501713117323, 10.36367586454735, 10.94724501508226, 11.46059121971409, 11.70710125745063, 12.18891049595484, 12.73072197054595, 13.49676938325751, 13.82104131827494, 14.46623890855581, 14.95134465544795