↑

Properties

Label 1-95-95.92-r1-0-0
Degree $1$
Conductor $95$
Sign $-0.0451 + 0.998i$
Analytic cond. $10.2091$
Root an. cond. $10.2091$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−0.984 + 0.173i)2-s + (−0.642 − 0.766i)3-s + (0.939 − 0.342i)4-s + (0.766 + 0.642i)6-s + (−0.866 − 0.5i)7-s + (−0.866 + 0.5i)8-s + (−0.173 + 0.984i)9-s + (−0.5 − 0.866i)11-s + (−0.866 − 0.5i)12-s + (0.642 − 0.766i)13-s + (0.939 + 0.342i)14-s + (0.766 − 0.642i)16-s + (−0.984 + 0.173i)17-s − i·18-s + (0.173 + 0.984i)21-s + (0.642 + 0.766i)22-s + ⋯
L(s)  = 1  + (−0.984 + 0.173i)2-s + (−0.642 − 0.766i)3-s + (0.939 − 0.342i)4-s + (0.766 + 0.642i)6-s + (−0.866 − 0.5i)7-s + (−0.866 + 0.5i)8-s + (−0.173 + 0.984i)9-s + (−0.5 − 0.866i)11-s + (−0.866 − 0.5i)12-s + (0.642 − 0.766i)13-s + (0.939 + 0.342i)14-s + (0.766 − 0.642i)16-s + (−0.984 + 0.173i)17-s − i·18-s + (0.173 + 0.984i)21-s + (0.642 + 0.766i)22-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 95 ^{s/2} \, \Gamma_{\R}(s+1) \, L(s)\cr =\mathstrut & (-0.0451 + 0.998i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 95 ^{s/2} \, \Gamma_{\R}(s+1) \, L(s)\cr =\mathstrut & (-0.0451 + 0.998i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(1\)
Conductor: \(95\)    =    \(5 \cdot 19\)
Sign: $-0.0451 + 0.998i$
Analytic conductor: \(10.2091\)
Root analytic conductor: \(10.2091\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{95} (92, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((1,\ 95,\ (1:\ ),\ -0.0451 + 0.998i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.1436520836 + 0.1502856956i\)
\(L(\frac12)\) \(\approx\) \(0.1436520836 + 0.1502856956i\)
\(L(1)\) \(\approx\) \(0.4282553284 - 0.07429059458i\)
\(L(1)\) \(\approx\) \(0.4282553284 - 0.07429059458i\)

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad5 \( 1 \)
19 \( 1 \)
good2 \( 1 + (-0.984 + 0.173i)T \)
3 \( 1 + (-0.642 - 0.766i)T \)
7 \( 1 + (-0.866 - 0.5i)T \)
11 \( 1 + (-0.5 - 0.866i)T \)
13 \( 1 + (0.642 - 0.766i)T \)
17 \( 1 + (-0.984 + 0.173i)T \)
23 \( 1 + (0.342 + 0.939i)T \)
29 \( 1 + (-0.173 + 0.984i)T \)
31 \( 1 + (-0.5 + 0.866i)T \)
37 \( 1 + iT \)
41 \( 1 + (0.766 - 0.642i)T \)
43 \( 1 + (-0.342 + 0.939i)T \)
47 \( 1 + (0.984 + 0.173i)T \)
53 \( 1 + (0.342 + 0.939i)T \)
59 \( 1 + (-0.173 - 0.984i)T \)
61 \( 1 + (-0.939 + 0.342i)T \)
67 \( 1 + (0.984 + 0.173i)T \)
71 \( 1 + (-0.939 - 0.342i)T \)
73 \( 1 + (-0.642 - 0.766i)T \)
79 \( 1 + (-0.766 + 0.642i)T \)
83 \( 1 + (0.866 + 0.5i)T \)
89 \( 1 + (-0.766 - 0.642i)T \)
97 \( 1 + (-0.984 + 0.173i)T \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ (1 - \alpha_{p}\, p^{-s})^{-1}\)

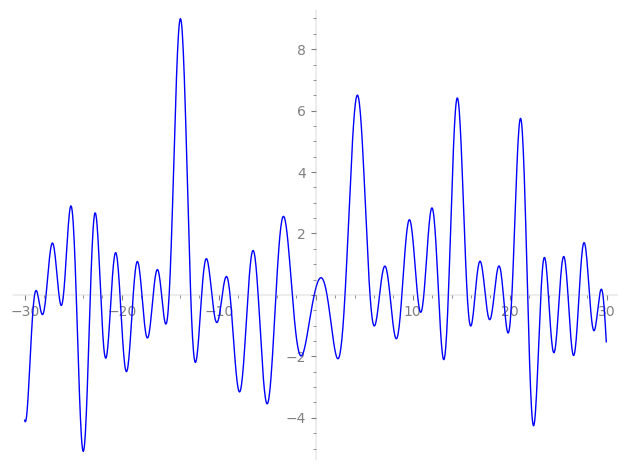
Imaginary part of the first few zeros on the critical line

−28.98207773829777556462098702207, −28.64620442062038688021277548182, −27.79473234980270382714075231076, −26.46597324209583734090848817216, −26.001659616700418680822838293722, −24.68672870966788838053691453419, −23.233670971268265299863330672420, −22.16059673645781580087053050218, −21.07716623454390098936151145511, −20.17532364676240719416143179907, −18.81161269493234259520004378751, −17.91540886093386327651935445586, −16.75248617732612879162796910551, −15.88786249077670719304804100951, −15.10830166560752309934109080180, −12.887228404319183504174151722832, −11.75955261472416264979917393433, −10.70369060064943568160829002882, −9.63116013788155677338138631695, −8.83377921553808442683990748986, −6.98453444571699646198474453849, −5.93498314677774285899199666290, −4.10282439469411230378226608506, −2.41258825556532452438266435794, −0.15518387887657380654473755102, 1.16225815372873234039051529892, 3.01812984420647006410439813981, 5.59641487452379385536890181018, 6.58408259083114614173576690756, 7.65157725652973523181411817443, 8.8805329070016079178899259681, 10.49446631512216074692268867514, 11.14330033557221085818200844883, 12.66743581375039627476725981991, 13.67297813569562799299730140174, 15.61667657476936079905809927336, 16.42722451519169957063327377927, 17.48034766461596565548568706886, 18.39389439070306364600676040959, 19.34335187342176277943929746003, 20.22214943951463734361671605533, 21.84342577904824549139746254562, 23.205890710466354952890694488867, 23.985468045312825624233939621947, 25.1188035496286303116888543477, 26.00084504398287557169846927817, 27.146122014673284149389232200670, 28.22306528457869866498943386305, 29.26158723496086771981993327484, 29.6037496225037409061991213510

Graph of the $Z$-function along the critical line