| L(s) = 1 | + 4·2-s + 4·4-s − 16·8-s − 80·11-s − 64·16-s − 320·22-s − 136·23-s + 200·25-s + 440·29-s − 64·32-s + 40·37-s − 1.36e3·43-s − 320·44-s − 544·46-s + 800·50-s − 1.25e3·53-s + 1.76e3·58-s + 192·64-s − 1.08e3·67-s − 1.68e3·71-s + 160·74-s + 1.52e3·79-s − 5.44e3·86-s + 1.28e3·88-s − 544·92-s + 800·100-s − 5.02e3·106-s + ⋯ |
| L(s) = 1 | + 1.41·2-s + 1/2·4-s − 0.707·8-s − 2.19·11-s − 16-s − 3.10·22-s − 1.23·23-s + 8/5·25-s + 2.81·29-s − 0.353·32-s + 0.177·37-s − 4.82·43-s − 1.09·44-s − 1.74·46-s + 2.26·50-s − 3.25·53-s + 3.98·58-s + 3/8·64-s − 1.96·67-s − 2.80·71-s + 0.251·74-s + 2.16·79-s − 6.82·86-s + 1.55·88-s − 0.616·92-s + 4/5·100-s − 4.60·106-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{4} \cdot 3^{8} \cdot 7^{8}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(4-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{4} \cdot 3^{8} \cdot 7^{8}\right)^{s/2} \, \Gamma_{\C}(s+3/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(2)\) |
\(\approx\) |
\(0.1250527643\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.1250527643\) |
| \(L(\frac{5}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_2$ | \( ( 1 - p T + p^{2} T^{2} )^{2} \) |
| 3 | | \( 1 \) |
| 7 | | \( 1 \) |
| good | 5 | $C_2^3$ | \( 1 - 8 p^{2} T^{2} + 39 p^{4} T^{4} - 8 p^{8} T^{6} + p^{12} T^{8} \) |
| 11 | $C_2^2$ | \( ( 1 + 40 T + 269 T^{2} + 40 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 13 | $C_2^2$ | \( ( 1 + 344 T^{2} + p^{6} T^{4} )^{2} \) |
| 17 | $C_2^3$ | \( 1 - 9824 T^{2} + 72373407 T^{4} - 9824 p^{6} T^{6} + p^{12} T^{8} \) |
| 19 | $C_2^3$ | \( 1 - 13590 T^{2} + 137642219 T^{4} - 13590 p^{6} T^{6} + p^{12} T^{8} \) |
| 23 | $C_2^2$ | \( ( 1 + 68 T - 7543 T^{2} + 68 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 29 | $C_2$ | \( ( 1 - 110 T + p^{3} T^{2} )^{4} \) |
| 31 | $C_2^3$ | \( 1 - 45470 T^{2} + 1180017219 T^{4} - 45470 p^{6} T^{6} + p^{12} T^{8} \) |
| 37 | $C_2^2$ | \( ( 1 - 20 T - 50253 T^{2} - 20 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 41 | $C_2^2$ | \( ( 1 + 135392 T^{2} + p^{6} T^{4} )^{2} \) |
| 43 | $C_2$ | \( ( 1 + 340 T + p^{3} T^{2} )^{4} \) |
| 47 | $C_2^3$ | \( 1 - 199454 T^{2} + 29002682787 T^{4} - 199454 p^{6} T^{6} + p^{12} T^{8} \) |
| 53 | $C_2^2$ | \( ( 1 + 628 T + 245507 T^{2} + 628 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 59 | $C_2^3$ | \( 1 + 358042 T^{2} + 86013540123 T^{4} + 358042 p^{6} T^{6} + p^{12} T^{8} \) |
| 61 | $C_2^3$ | \( 1 + 388440 T^{2} + 99365259239 T^{4} + 388440 p^{6} T^{6} + p^{12} T^{8} \) |
| 67 | $C_2^2$ | \( ( 1 + 540 T - 9163 T^{2} + 540 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 71 | $C_2$ | \( ( 1 + 420 T + p^{3} T^{2} )^{4} \) |
| 73 | $C_2^3$ | \( 1 - 693984 T^{2} + 330279565967 T^{4} - 693984 p^{6} T^{6} + p^{12} T^{8} \) |
| 79 | $C_2^2$ | \( ( 1 - 760 T + 84561 T^{2} - 760 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 83 | $C_2^2$ | \( ( 1 + 251126 T^{2} + p^{6} T^{4} )^{2} \) |
| 89 | $C_2^3$ | \( 1 - 81488 T^{2} - 490340996817 T^{4} - 81488 p^{6} T^{6} + p^{12} T^{8} \) |
| 97 | $C_2^2$ | \( ( 1 + 1573296 T^{2} + p^{6} T^{4} )^{2} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
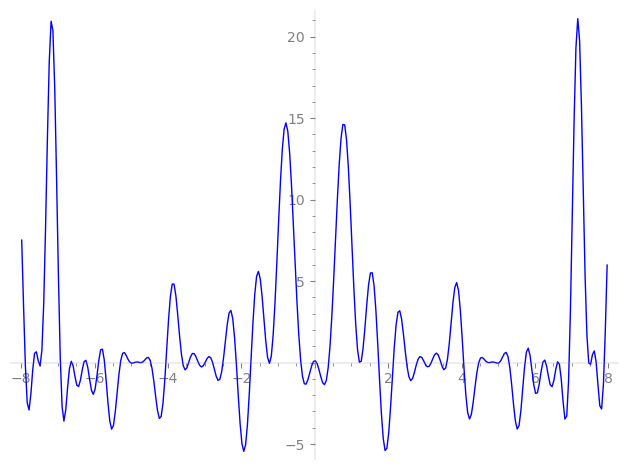
Imaginary part of the first few zeros on the critical line
−6.65400599247644922511870581702, −6.60666192671680663418519894785, −6.29381030339175686200967985491, −6.21268011240786917290888159233, −5.89198440244165069461467849223, −5.72783163910242678149509870117, −5.29528577687905139123514401920, −5.02671289481431851270752577012, −4.91860640785232690327732117628, −4.76263510849454816735267671287, −4.72012895475227208174700616939, −4.46712563938481778299090351592, −4.05606176389638289637154961133, −3.60060281431077958403596512462, −3.43573206677120531196063393186, −3.17300048396567880328788575480, −2.98880761201439101731499402306, −2.78322656430347798432188479229, −2.50076238384072607333124291481, −2.13880586113806503739074490906, −1.74098714268034702512554026458, −1.25438283622205375652381472402, −1.21887729345773790829846440741, −0.37906806226587119201680175172, −0.05156449302397461625119695444,
0.05156449302397461625119695444, 0.37906806226587119201680175172, 1.21887729345773790829846440741, 1.25438283622205375652381472402, 1.74098714268034702512554026458, 2.13880586113806503739074490906, 2.50076238384072607333124291481, 2.78322656430347798432188479229, 2.98880761201439101731499402306, 3.17300048396567880328788575480, 3.43573206677120531196063393186, 3.60060281431077958403596512462, 4.05606176389638289637154961133, 4.46712563938481778299090351592, 4.72012895475227208174700616939, 4.76263510849454816735267671287, 4.91860640785232690327732117628, 5.02671289481431851270752577012, 5.29528577687905139123514401920, 5.72783163910242678149509870117, 5.89198440244165069461467849223, 6.21268011240786917290888159233, 6.29381030339175686200967985491, 6.60666192671680663418519894785, 6.65400599247644922511870581702