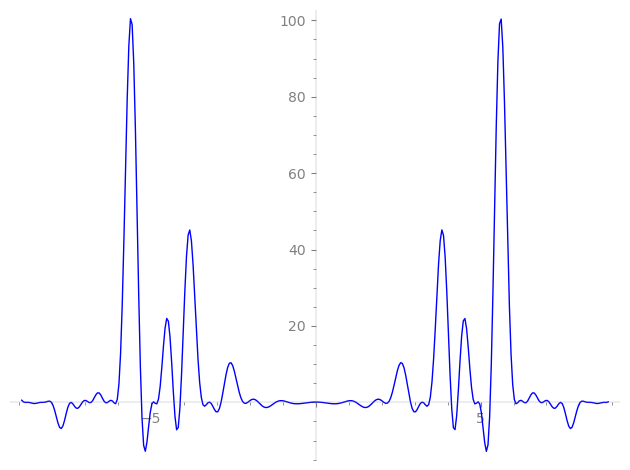
| L(s) = 1 | − 4·2-s + 8·4-s − 4·7-s − 8·8-s + 16·14-s − 4·16-s − 4·23-s − 32·28-s + 20·29-s + 32·32-s − 44·43-s + 16·46-s − 2·49-s + 32·56-s − 80·58-s − 64·64-s + 12·67-s − 18·81-s + 176·86-s − 32·92-s + 8·98-s + 32·107-s + 60·109-s + 16·112-s + 160·116-s − 6·121-s + 127-s + ⋯ |
| L(s) = 1 | − 2.82·2-s + 4·4-s − 1.51·7-s − 2.82·8-s + 4.27·14-s − 16-s − 0.834·23-s − 6.04·28-s + 3.71·29-s + 5.65·32-s − 6.70·43-s + 2.35·46-s − 2/7·49-s + 4.27·56-s − 10.5·58-s − 8·64-s + 1.46·67-s − 2·81-s + 18.9·86-s − 3.33·92-s + 0.808·98-s + 3.09·107-s + 5.74·109-s + 1.51·112-s + 14.8·116-s − 0.545·121-s + 0.0887·127-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{8} \cdot 5^{8} \cdot 7^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(2-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{8} \cdot 5^{8} \cdot 7^{4}\right)^{s/2} \, \Gamma_{\C}(s+1/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(0.08531349876\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.08531349876\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_2$ | \( ( 1 + p T + p T^{2} )^{2} \) |
| 5 | | \( 1 \) |
| 7 | $C_2$ | \( ( 1 + 2 T + p T^{2} )^{2} \) |
| good | 3 | $C_2^2$ | \( ( 1 + p^{2} T^{4} )^{2} \) |
| 11 | $C_2^2$ | \( ( 1 + 3 T^{2} + p^{2} T^{4} )^{2} \) |
| 13 | $C_2^2$ | \( ( 1 + 20 T^{2} + p^{2} T^{4} )^{2} \) |
| 17 | $C_2^2$ | \( ( 1 + 10 T^{2} + p^{2} T^{4} )^{2} \) |
| 19 | $C_2$ | \( ( 1 + p T^{2} )^{4} \) |
| 23 | $C_2$ | \( ( 1 + T + p T^{2} )^{4} \) |
| 29 | $C_2$ | \( ( 1 - 5 T + p T^{2} )^{4} \) |
| 31 | $C_2^2$ | \( ( 1 + 8 T^{2} + p^{2} T^{4} )^{2} \) |
| 37 | $C_2^2$ | \( ( 1 - 65 T^{2} + p^{2} T^{4} )^{2} \) |
| 41 | $C_2^2$ | \( ( 1 + 68 T^{2} + p^{2} T^{4} )^{2} \) |
| 43 | $C_2$ | \( ( 1 + 11 T + p T^{2} )^{4} \) |
| 47 | $C_2^2$ | \( ( 1 - 70 T^{2} + p^{2} T^{4} )^{2} \) |
| 53 | $C_2$ | \( ( 1 - 14 T + p T^{2} )^{2}( 1 + 14 T + p T^{2} )^{2} \) |
| 59 | $C_2^2$ | \( ( 1 - 32 T^{2} + p^{2} T^{4} )^{2} \) |
| 61 | $C_2^2$ | \( ( 1 + 28 T^{2} + p^{2} T^{4} )^{2} \) |
| 67 | $C_2$ | \( ( 1 - 3 T + p T^{2} )^{4} \) |
| 71 | $C_2^2$ | \( ( 1 - 117 T^{2} + p^{2} T^{4} )^{2} \) |
| 73 | $C_2^2$ | \( ( 1 + 140 T^{2} + p^{2} T^{4} )^{2} \) |
| 79 | $C_2^2$ | \( ( 1 - 77 T^{2} + p^{2} T^{4} )^{2} \) |
| 83 | $C_2^2$ | \( ( 1 - 160 T^{2} + p^{2} T^{4} )^{2} \) |
| 89 | $C_2^2$ | \( ( 1 - 172 T^{2} + p^{2} T^{4} )^{2} \) |
| 97 | $C_2^2$ | \( ( 1 + 140 T^{2} + p^{2} T^{4} )^{2} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−7.43682482600369517638195388443, −7.42641557209902586737057996713, −7.08684948045845682130025427804, −6.89070177980392820890008859170, −6.81720838421729738503968428847, −6.39548296638332241740208188831, −6.31628382333336540659434826476, −6.13500724509747292012278700101, −6.04746270182600918334889341751, −5.29208683329478640771215784511, −4.95334382961862985307434193233, −4.89857709992370256171778083501, −4.79964732481931439554506576631, −4.30397711727848389678941555694, −4.11424542553821051055063356186, −3.44616769979758323797794276976, −3.25674459130478828005607176175, −3.20676965909006776525020044636, −2.87589362058556018888713648461, −2.20112813303573228190374159614, −2.06685534072767990501392757166, −1.73819859360698334423726265906, −1.22102541568391849971256756268, −0.825728559347057657812503843887, −0.17987227981376109836873039345,
0.17987227981376109836873039345, 0.825728559347057657812503843887, 1.22102541568391849971256756268, 1.73819859360698334423726265906, 2.06685534072767990501392757166, 2.20112813303573228190374159614, 2.87589362058556018888713648461, 3.20676965909006776525020044636, 3.25674459130478828005607176175, 3.44616769979758323797794276976, 4.11424542553821051055063356186, 4.30397711727848389678941555694, 4.79964732481931439554506576631, 4.89857709992370256171778083501, 4.95334382961862985307434193233, 5.29208683329478640771215784511, 6.04746270182600918334889341751, 6.13500724509747292012278700101, 6.31628382333336540659434826476, 6.39548296638332241740208188831, 6.81720838421729738503968428847, 6.89070177980392820890008859170, 7.08684948045845682130025427804, 7.42641557209902586737057996713, 7.43682482600369517638195388443