| L(s) = 1 | + 4·5-s + 8·25-s + 4·29-s + 4·53-s − 81-s − 8·97-s + 4·101-s + 12·125-s + 127-s + 131-s + 137-s + 139-s + 16·145-s + 149-s + 151-s + 157-s + 163-s + 167-s + 173-s + 179-s + 181-s + 191-s + 193-s + 197-s + 199-s + 211-s + 223-s + ⋯ |
| L(s) = 1 | + 4·5-s + 8·25-s + 4·29-s + 4·53-s − 81-s − 8·97-s + 4·101-s + 12·125-s + 127-s + 131-s + 137-s + 139-s + 16·145-s + 149-s + 151-s + 157-s + 163-s + 167-s + 173-s + 179-s + 181-s + 191-s + 193-s + 197-s + 199-s + 211-s + 223-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{40} \cdot 3^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{40} \cdot 3^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(\frac{1}{2})\) |
\(\approx\) |
\(5.151445737\) |
| \(L(\frac12)\) |
\(\approx\) |
\(5.151445737\) |
| \(L(1)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | | \( 1 \) |
| 3 | $C_2^2$ | \( 1 + T^{4} \) |
| good | 5 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{4}( 1 + T^{2} )^{2} \) |
| 7 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 11 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 13 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 17 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 19 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 23 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 29 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{4}( 1 + T^{2} )^{2} \) |
| 31 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 37 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 41 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 43 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 47 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 53 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{4}( 1 + T^{2} )^{2} \) |
| 59 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 61 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 67 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 71 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 73 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 79 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 83 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 89 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 97 | $C_1$ | \( ( 1 + T )^{8} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
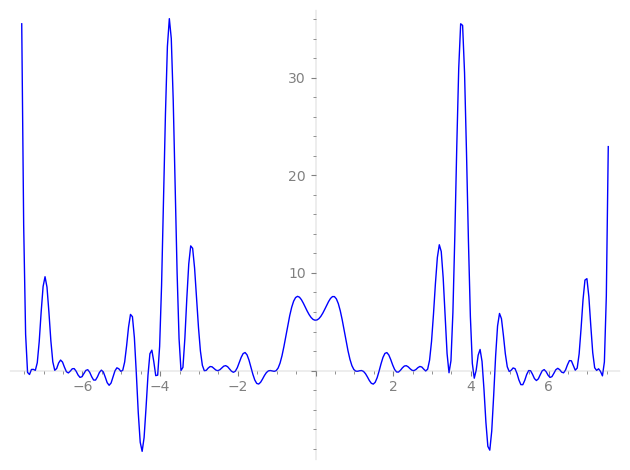
Imaginary part of the first few zeros on the critical line
−6.30316039865065811692633334538, −6.17259652628470540877831807922, −5.91670545090749496973089760558, −5.83972136251799428852648814744, −5.53244551160912387720814522941, −5.48624913155813880209990266209, −5.16052111905534477347100105754, −5.03078800469277393504516950514, −4.96602860971618869624204441395, −4.61715759243337261069415793406, −4.30521829959841082469608134852, −4.13468988420988663562583351683, −4.05031999766707573593851654903, −3.46369972840480522571364315768, −3.42409462183955206607210737542, −2.86688605358286930455247893522, −2.81839659550972779658887060070, −2.54116998413610041546289081331, −2.49897956678911766965327139983, −2.17995600944609962171415975583, −2.05239348523040099847752966227, −1.63983652320964928946055910882, −1.18769800524870273713950342010, −1.15830482563995193885761785435, −1.01078294170993759154394353789,
1.01078294170993759154394353789, 1.15830482563995193885761785435, 1.18769800524870273713950342010, 1.63983652320964928946055910882, 2.05239348523040099847752966227, 2.17995600944609962171415975583, 2.49897956678911766965327139983, 2.54116998413610041546289081331, 2.81839659550972779658887060070, 2.86688605358286930455247893522, 3.42409462183955206607210737542, 3.46369972840480522571364315768, 4.05031999766707573593851654903, 4.13468988420988663562583351683, 4.30521829959841082469608134852, 4.61715759243337261069415793406, 4.96602860971618869624204441395, 5.03078800469277393504516950514, 5.16052111905534477347100105754, 5.48624913155813880209990266209, 5.53244551160912387720814522941, 5.83972136251799428852648814744, 5.91670545090749496973089760558, 6.17259652628470540877831807922, 6.30316039865065811692633334538