| L(s) = 1 | − 4-s + 6·9-s − 3·16-s + 16·19-s − 10·25-s − 6·36-s − 28·49-s + 7·64-s − 16·76-s + 27·81-s + 10·100-s + 44·121-s + 127-s + 131-s + 137-s + 139-s − 18·144-s + 149-s + 151-s + 157-s + 163-s + 167-s − 52·169-s + 96·171-s + 173-s + 179-s + 181-s + ⋯ |
| L(s) = 1 | − 1/2·4-s + 2·9-s − 3/4·16-s + 3.67·19-s − 2·25-s − 36-s − 4·49-s + 7/8·64-s − 1.83·76-s + 3·81-s + 100-s + 4·121-s + 0.0887·127-s + 0.0873·131-s + 0.0854·137-s + 0.0848·139-s − 3/2·144-s + 0.0819·149-s + 0.0813·151-s + 0.0798·157-s + 0.0783·163-s + 0.0773·167-s − 4·169-s + 7.34·171-s + 0.0760·173-s + 0.0747·179-s + 0.0743·181-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{12} \cdot 3^{4} \cdot 5^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(2-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{12} \cdot 3^{4} \cdot 5^{4}\right)^{s/2} \, \Gamma_{\C}(s+1/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(1.162814256\) |
| \(L(\frac12)\) |
\(\approx\) |
\(1.162814256\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_2^2$ | \( 1 + T^{2} + p^{2} T^{4} \) |
| 3 | $C_2$ | \( ( 1 - p T^{2} )^{2} \) |
| 5 | $C_2$ | \( ( 1 + p T^{2} )^{2} \) |
| good | 7 | $C_2$ | \( ( 1 + p T^{2} )^{4} \) |
| 11 | $C_2$ | \( ( 1 - p T^{2} )^{4} \) |
| 13 | $C_2$ | \( ( 1 + p T^{2} )^{4} \) |
| 17 | $C_2^2$ | \( ( 1 - 14 T^{2} + p^{2} T^{4} )^{2} \) |
| 19 | $C_2$ | \( ( 1 - 4 T + p T^{2} )^{4} \) |
| 23 | $C_2^2$ | \( ( 1 + 34 T^{2} + p^{2} T^{4} )^{2} \) |
| 29 | $C_2$ | \( ( 1 + p T^{2} )^{4} \) |
| 31 | $C_2$ | \( ( 1 - 8 T + p T^{2} )^{2}( 1 + 8 T + p T^{2} )^{2} \) |
| 37 | $C_2$ | \( ( 1 + p T^{2} )^{4} \) |
| 41 | $C_2$ | \( ( 1 - p T^{2} )^{4} \) |
| 43 | $C_2$ | \( ( 1 - p T^{2} )^{4} \) |
| 47 | $C_2^2$ | \( ( 1 - 14 T^{2} + p^{2} T^{4} )^{2} \) |
| 53 | $C_2^2$ | \( ( 1 - 86 T^{2} + p^{2} T^{4} )^{2} \) |
| 59 | $C_2$ | \( ( 1 - p T^{2} )^{4} \) |
| 61 | $C_2$ | \( ( 1 - 2 T + p T^{2} )^{2}( 1 + 2 T + p T^{2} )^{2} \) |
| 67 | $C_2$ | \( ( 1 - p T^{2} )^{4} \) |
| 71 | $C_2$ | \( ( 1 + p T^{2} )^{4} \) |
| 73 | $C_2$ | \( ( 1 - p T^{2} )^{4} \) |
| 79 | $C_2$ | \( ( 1 - 16 T + p T^{2} )^{2}( 1 + 16 T + p T^{2} )^{2} \) |
| 83 | $C_2^2$ | \( ( 1 + 154 T^{2} + p^{2} T^{4} )^{2} \) |
| 89 | $C_2$ | \( ( 1 - p T^{2} )^{4} \) |
| 97 | $C_2$ | \( ( 1 - p T^{2} )^{4} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
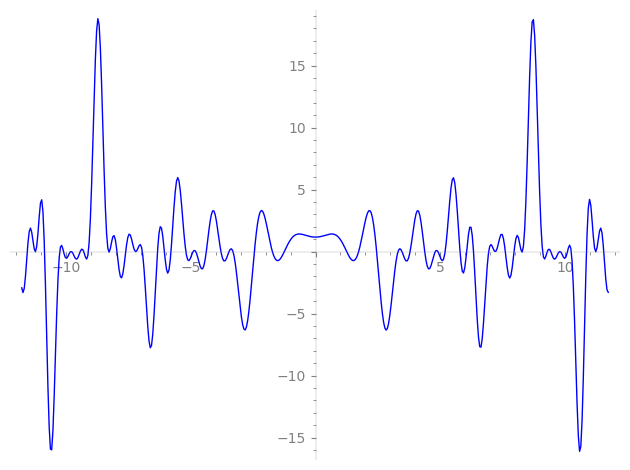
Imaginary part of the first few zeros on the critical line
−9.808524879053431654339438705285, −9.772644300205767193251000508362, −9.426464548989252731432720387646, −9.287519628760410954942504180246, −9.100050428973946658486016822351, −8.293006408197617641650026815652, −8.252627641704206271703064071715, −7.955335915614753098599944535934, −7.60429980742977750577878436097, −7.21442206638901471156076448920, −7.18814680219832983582668286538, −6.93955839577251695221461704680, −6.33051875775614412315787853556, −6.05532064796848729882870449626, −5.79089491580389829527964502812, −5.19345208285814782747346326183, −4.90396513482860089923114534067, −4.79833409731623754548422130776, −4.37537421501178733384641744417, −3.78898483280470033170864145423, −3.46359795232067585996238519145, −3.30604674302533284706138136287, −2.44853504103337796203918483388, −1.72819469709323362843672116265, −1.24871830823032357325157849446,
1.24871830823032357325157849446, 1.72819469709323362843672116265, 2.44853504103337796203918483388, 3.30604674302533284706138136287, 3.46359795232067585996238519145, 3.78898483280470033170864145423, 4.37537421501178733384641744417, 4.79833409731623754548422130776, 4.90396513482860089923114534067, 5.19345208285814782747346326183, 5.79089491580389829527964502812, 6.05532064796848729882870449626, 6.33051875775614412315787853556, 6.93955839577251695221461704680, 7.18814680219832983582668286538, 7.21442206638901471156076448920, 7.60429980742977750577878436097, 7.955335915614753098599944535934, 8.252627641704206271703064071715, 8.293006408197617641650026815652, 9.100050428973946658486016822351, 9.287519628760410954942504180246, 9.426464548989252731432720387646, 9.772644300205767193251000508362, 9.808524879053431654339438705285