| L(s) = 1 | + 4-s − 8·5-s − 2·11-s − 2·19-s − 8·20-s + 38·25-s − 20·29-s − 16·31-s − 12·41-s − 2·44-s − 13·49-s + 16·55-s + 16·59-s + 16·61-s − 64-s − 8·71-s − 2·76-s − 40·79-s − 6·89-s + 16·95-s + 38·100-s + 20·101-s + 24·109-s − 20·116-s + 23·121-s − 16·124-s − 136·125-s + ⋯ |
| L(s) = 1 | + 1/2·4-s − 3.57·5-s − 0.603·11-s − 0.458·19-s − 1.78·20-s + 38/5·25-s − 3.71·29-s − 2.87·31-s − 1.87·41-s − 0.301·44-s − 1.85·49-s + 2.15·55-s + 2.08·59-s + 2.04·61-s − 1/8·64-s − 0.949·71-s − 0.229·76-s − 4.50·79-s − 0.635·89-s + 1.64·95-s + 19/5·100-s + 1.99·101-s + 2.29·109-s − 1.85·116-s + 2.09·121-s − 1.43·124-s − 12.1·125-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{4} \cdot 3^{8} \cdot 5^{4} \cdot 13^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(2-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{4} \cdot 3^{8} \cdot 5^{4} \cdot 13^{4}\right)^{s/2} \, \Gamma_{\C}(s+1/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(0.2651837645\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.2651837645\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_2^2$ | \( 1 - T^{2} + T^{4} \) |
| 3 | | \( 1 \) |
| 5 | $C_2$ | \( ( 1 + 4 T + p T^{2} )^{2} \) |
| 13 | $C_2^2$ | \( 1 + 23 T^{2} + p^{2} T^{4} \) |
| good | 7 | $C_2^2$$\times$$C_2^2$ | \( ( 1 + 2 T^{2} + p^{2} T^{4} )( 1 + 11 T^{2} + p^{2} T^{4} ) \) |
| 11 | $C_2^2$ | \( ( 1 + T - 10 T^{2} + p T^{3} + p^{2} T^{4} )^{2} \) |
| 17 | $C_2^3$ | \( 1 + 18 T^{2} + 35 T^{4} + 18 p^{2} T^{6} + p^{4} T^{8} \) |
| 19 | $C_2$ | \( ( 1 - 7 T + p T^{2} )^{2}( 1 + 8 T + p T^{2} )^{2} \) |
| 23 | $C_2^2$ | \( ( 1 + p T^{2} + p^{2} T^{4} )^{2} \) |
| 29 | $C_2^2$ | \( ( 1 + 10 T + 71 T^{2} + 10 p T^{3} + p^{2} T^{4} )^{2} \) |
| 31 | $C_2$ | \( ( 1 + 4 T + p T^{2} )^{4} \) |
| 37 | $C_2^3$ | \( 1 + 65 T^{2} + 2856 T^{4} + 65 p^{2} T^{6} + p^{4} T^{8} \) |
| 41 | $C_2^2$ | \( ( 1 + 6 T - 5 T^{2} + 6 p T^{3} + p^{2} T^{4} )^{2} \) |
| 43 | $C_2^3$ | \( 1 + 70 T^{2} + 3051 T^{4} + 70 p^{2} T^{6} + p^{4} T^{8} \) |
| 47 | $C_2^2$ | \( ( 1 - 45 T^{2} + p^{2} T^{4} )^{2} \) |
| 53 | $C_2^2$ | \( ( 1 + 15 T^{2} + p^{2} T^{4} )^{2} \) |
| 59 | $C_2^2$ | \( ( 1 - 8 T + 5 T^{2} - 8 p T^{3} + p^{2} T^{4} )^{2} \) |
| 61 | $C_2^2$ | \( ( 1 - 8 T + 3 T^{2} - 8 p T^{3} + p^{2} T^{4} )^{2} \) |
| 67 | $C_2^3$ | \( 1 + 130 T^{2} + 12411 T^{4} + 130 p^{2} T^{6} + p^{4} T^{8} \) |
| 71 | $C_2^2$ | \( ( 1 + 4 T - 55 T^{2} + 4 p T^{3} + p^{2} T^{4} )^{2} \) |
| 73 | $C_2^2$ | \( ( 1 - 82 T^{2} + p^{2} T^{4} )^{2} \) |
| 79 | $C_2$ | \( ( 1 + 10 T + p T^{2} )^{4} \) |
| 83 | $C_2^2$ | \( ( 1 + 158 T^{2} + p^{2} T^{4} )^{2} \) |
| 89 | $C_2^2$ | \( ( 1 + 3 T - 80 T^{2} + 3 p T^{3} + p^{2} T^{4} )^{2} \) |
| 97 | $C_2^3$ | \( 1 + 158 T^{2} + 15555 T^{4} + 158 p^{2} T^{6} + p^{4} T^{8} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
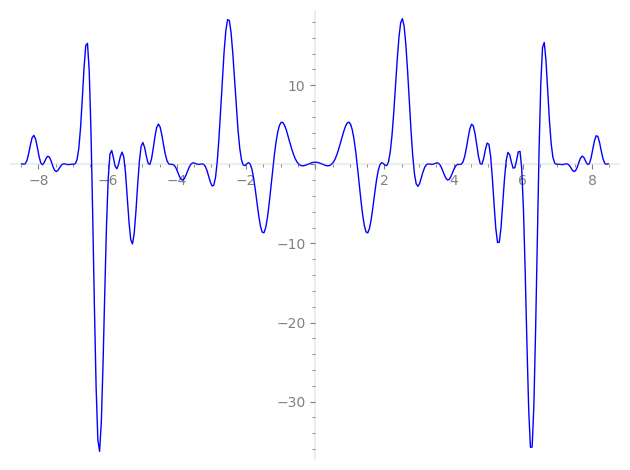
Imaginary part of the first few zeros on the critical line
−7.06808493312154392678169947435, −6.98499295191555092331991712135, −6.97620985420930019790765433246, −6.45987577433407175190709726417, −5.95936263258033768460081244414, −5.79584199961057292001377069760, −5.68306981784099055458418441048, −5.50568523150304171987041542319, −5.08928710666491858253894818318, −4.81646836085032070474291628042, −4.77645315763829989458876970390, −4.21658478025145559032394915832, −4.14117820249320460351641558683, −4.12521764169704254378870802118, −3.59494008506650607611055993655, −3.39718233709410254065277308353, −3.33843620264787119766808774119, −3.22605530706077306562686898431, −2.83873652378764366855240172030, −2.09204787043503446427951921966, −1.99185280347326619741024644373, −1.87497363410884586265219085418, −1.21151505400892189639481573550, −0.47131197575108846806461379100, −0.21698004197574195217583510936,
0.21698004197574195217583510936, 0.47131197575108846806461379100, 1.21151505400892189639481573550, 1.87497363410884586265219085418, 1.99185280347326619741024644373, 2.09204787043503446427951921966, 2.83873652378764366855240172030, 3.22605530706077306562686898431, 3.33843620264787119766808774119, 3.39718233709410254065277308353, 3.59494008506650607611055993655, 4.12521764169704254378870802118, 4.14117820249320460351641558683, 4.21658478025145559032394915832, 4.77645315763829989458876970390, 4.81646836085032070474291628042, 5.08928710666491858253894818318, 5.50568523150304171987041542319, 5.68306981784099055458418441048, 5.79584199961057292001377069760, 5.95936263258033768460081244414, 6.45987577433407175190709726417, 6.97620985420930019790765433246, 6.98499295191555092331991712135, 7.06808493312154392678169947435