| L(s) = 1 | − 2·2-s − 7·3-s + 8·4-s − 7·5-s + 14·6-s + 28·7-s − 40·8-s + 27·9-s + 14·10-s + 5·11-s − 56·12-s − 28·13-s − 56·14-s + 49·15-s + 80·16-s + 21·17-s − 54·18-s − 49·19-s − 56·20-s − 196·21-s − 10·22-s + 159·23-s + 280·24-s + 125·25-s + 56·26-s − 224·27-s + 224·28-s + ⋯ |
| L(s) = 1 | − 0.707·2-s − 1.34·3-s + 4-s − 0.626·5-s + 0.952·6-s + 1.51·7-s − 1.76·8-s + 9-s + 0.442·10-s + 0.137·11-s − 1.34·12-s − 0.597·13-s − 1.06·14-s + 0.843·15-s + 5/4·16-s + 0.299·17-s − 0.707·18-s − 0.591·19-s − 0.626·20-s − 2.03·21-s − 0.0969·22-s + 1.44·23-s + 2.38·24-s + 25-s + 0.422·26-s − 1.59·27-s + 1.51·28-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 49 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(4-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 49 ^{s/2} \, \Gamma_{\C}(s+3/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(2)\) |
\(\approx\) |
\(0.3572712451\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.3572712451\) |
| \(L(\frac{5}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 7 | $C_2$ | \( 1 - 4 p T + p^{3} T^{2} \) |
| good | 2 | $C_2^2$ | \( 1 + p T - p^{2} T^{2} + p^{4} T^{3} + p^{6} T^{4} \) |
| 3 | $C_2^2$ | \( 1 + 7 T + 22 T^{2} + 7 p^{3} T^{3} + p^{6} T^{4} \) |
| 5 | $C_2^2$ | \( 1 + 7 T - 76 T^{2} + 7 p^{3} T^{3} + p^{6} T^{4} \) |
| 11 | $C_2^2$ | \( 1 - 5 T - 1306 T^{2} - 5 p^{3} T^{3} + p^{6} T^{4} \) |
| 13 | $C_2$ | \( ( 1 + 14 T + p^{3} T^{2} )^{2} \) |
| 17 | $C_2^2$ | \( 1 - 21 T - 4472 T^{2} - 21 p^{3} T^{3} + p^{6} T^{4} \) |
| 19 | $C_2^2$ | \( 1 + 49 T - 4458 T^{2} + 49 p^{3} T^{3} + p^{6} T^{4} \) |
| 23 | $C_2^2$ | \( 1 - 159 T + 13114 T^{2} - 159 p^{3} T^{3} + p^{6} T^{4} \) |
| 29 | $C_2$ | \( ( 1 - 2 p T + p^{3} T^{2} )^{2} \) |
| 31 | $C_2^2$ | \( 1 + 147 T - 8182 T^{2} + 147 p^{3} T^{3} + p^{6} T^{4} \) |
| 37 | $C_2^2$ | \( 1 + 219 T - 2692 T^{2} + 219 p^{3} T^{3} + p^{6} T^{4} \) |
| 41 | $C_2$ | \( ( 1 - 350 T + p^{3} T^{2} )^{2} \) |
| 43 | $C_2$ | \( ( 1 + 124 T + p^{3} T^{2} )^{2} \) |
| 47 | $C_2^2$ | \( 1 + 525 T + 171802 T^{2} + 525 p^{3} T^{3} + p^{6} T^{4} \) |
| 53 | $C_2^2$ | \( 1 + 303 T - 57068 T^{2} + 303 p^{3} T^{3} + p^{6} T^{4} \) |
| 59 | $C_2^2$ | \( 1 - 105 T - 194354 T^{2} - 105 p^{3} T^{3} + p^{6} T^{4} \) |
| 61 | $C_2^2$ | \( 1 - 413 T - 56412 T^{2} - 413 p^{3} T^{3} + p^{6} T^{4} \) |
| 67 | $C_2^2$ | \( 1 + 415 T - 128538 T^{2} + 415 p^{3} T^{3} + p^{6} T^{4} \) |
| 71 | $C_2$ | \( ( 1 + 432 T + p^{3} T^{2} )^{2} \) |
| 73 | $C_2^2$ | \( 1 - 1113 T + 849752 T^{2} - 1113 p^{3} T^{3} + p^{6} T^{4} \) |
| 79 | $C_2^2$ | \( 1 - 103 T - 482430 T^{2} - 103 p^{3} T^{3} + p^{6} T^{4} \) |
| 83 | $C_2$ | \( ( 1 - 1092 T + p^{3} T^{2} )^{2} \) |
| 89 | $C_2^2$ | \( 1 - 329 T - 596728 T^{2} - 329 p^{3} T^{3} + p^{6} T^{4} \) |
| 97 | $C_2$ | \( ( 1 + 882 T + p^{3} T^{2} )^{2} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
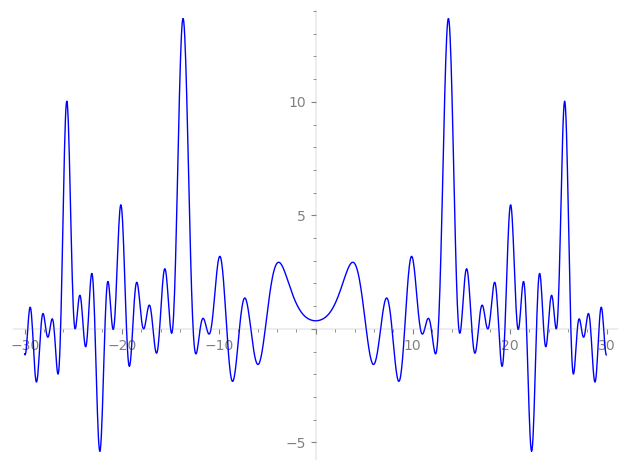
Imaginary part of the first few zeros on the critical line
−22.75658303906369405879076936982, −21.73262490716289823117921584584, −20.91822196939805874340971609810, −20.83702434468867677778925371131, −19.50153937985057617696689143507, −18.87238470644861754687131275082, −17.75884298513280071891956407611, −17.71699999773205043957589791903, −16.77242482888655925605925920086, −16.09259512717138983717111855239, −14.95994334252734381646800591924, −14.75073122826914210166577738781, −12.63773290481159472105769105934, −11.91232141937324149059092308649, −11.23114614585979948876648558038, −10.79042177854964714767970907634, −9.170771798623879815197307093822, −7.86320333232698952994279195127, −6.69000228021965412375783704525, −5.20239540052751869909136213505,
5.20239540052751869909136213505, 6.69000228021965412375783704525, 7.86320333232698952994279195127, 9.170771798623879815197307093822, 10.79042177854964714767970907634, 11.23114614585979948876648558038, 11.91232141937324149059092308649, 12.63773290481159472105769105934, 14.75073122826914210166577738781, 14.95994334252734381646800591924, 16.09259512717138983717111855239, 16.77242482888655925605925920086, 17.71699999773205043957589791903, 17.75884298513280071891956407611, 18.87238470644861754687131275082, 19.50153937985057617696689143507, 20.83702434468867677778925371131, 20.91822196939805874340971609810, 21.73262490716289823117921584584, 22.75658303906369405879076936982