| L(s) = 1 | + 2·2-s − 4·3-s − 8·6-s + 35·7-s − 8·8-s + 27·9-s − 30·11-s − 8·13-s + 70·14-s − 16·16-s − 9·17-s + 54·18-s + 88·19-s − 140·21-s − 60·22-s − 33·23-s + 32·24-s − 16·26-s − 260·27-s + 252·29-s − 155·31-s + 120·33-s − 18·34-s − 116·37-s + 176·38-s + 32·39-s − 846·41-s + ⋯ |
| L(s) = 1 | + 0.707·2-s − 0.769·3-s − 0.544·6-s + 1.88·7-s − 0.353·8-s + 9-s − 0.822·11-s − 0.170·13-s + 1.33·14-s − 1/4·16-s − 0.128·17-s + 0.707·18-s + 1.06·19-s − 1.45·21-s − 0.581·22-s − 0.299·23-s + 0.272·24-s − 0.120·26-s − 1.85·27-s + 1.61·29-s − 0.898·31-s + 0.633·33-s − 0.0907·34-s − 0.515·37-s + 0.751·38-s + 0.131·39-s − 3.22·41-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 122500 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(4-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 122500 ^{s/2} \, \Gamma_{\C}(s+3/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(2)\) |
\(\approx\) |
\(2.665621689\) |
| \(L(\frac12)\) |
\(\approx\) |
\(2.665621689\) |
| \(L(\frac{5}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_2$ | \( 1 - p T + p^{2} T^{2} \) |
| 5 | | \( 1 \) |
| 7 | $C_2$ | \( 1 - 5 p T + p^{3} T^{2} \) |
| good | 3 | $C_2^2$ | \( 1 + 4 T - 11 T^{2} + 4 p^{3} T^{3} + p^{6} T^{4} \) |
| 11 | $C_2^2$ | \( 1 + 30 T - 431 T^{2} + 30 p^{3} T^{3} + p^{6} T^{4} \) |
| 13 | $C_2$ | \( ( 1 + 4 T + p^{3} T^{2} )^{2} \) |
| 17 | $C_2^2$ | \( 1 + 9 T - 4832 T^{2} + 9 p^{3} T^{3} + p^{6} T^{4} \) |
| 19 | $C_2^2$ | \( 1 - 88 T + 885 T^{2} - 88 p^{3} T^{3} + p^{6} T^{4} \) |
| 23 | $C_2^2$ | \( 1 + 33 T - 11078 T^{2} + 33 p^{3} T^{3} + p^{6} T^{4} \) |
| 29 | $C_2$ | \( ( 1 - 126 T + p^{3} T^{2} )^{2} \) |
| 31 | $C_2^2$ | \( 1 + 5 p T - 6 p^{2} T^{2} + 5 p^{4} T^{3} + p^{6} T^{4} \) |
| 37 | $C_2^2$ | \( 1 + 116 T - 37197 T^{2} + 116 p^{3} T^{3} + p^{6} T^{4} \) |
| 41 | $C_2$ | \( ( 1 + 423 T + p^{3} T^{2} )^{2} \) |
| 43 | $C_2$ | \( ( 1 + 340 T + p^{3} T^{2} )^{2} \) |
| 47 | $C_2^2$ | \( 1 + 339 T + 11098 T^{2} + 339 p^{3} T^{3} + p^{6} T^{4} \) |
| 53 | $C_2^2$ | \( 1 - 312 T - 51533 T^{2} - 312 p^{3} T^{3} + p^{6} T^{4} \) |
| 59 | $C_2^2$ | \( 1 - 462 T + 8065 T^{2} - 462 p^{3} T^{3} + p^{6} T^{4} \) |
| 61 | $C_2^2$ | \( 1 + 326 T - 120705 T^{2} + 326 p^{3} T^{3} + p^{6} T^{4} \) |
| 67 | $C_2^2$ | \( 1 + 704 T + 194853 T^{2} + 704 p^{3} T^{3} + p^{6} T^{4} \) |
| 71 | $C_2$ | \( ( 1 - 621 T + p^{3} T^{2} )^{2} \) |
| 73 | $C_2^2$ | \( 1 - 250 T - 326517 T^{2} - 250 p^{3} T^{3} + p^{6} T^{4} \) |
| 79 | $C_2^2$ | \( 1 - 1105 T + 727986 T^{2} - 1105 p^{3} T^{3} + p^{6} T^{4} \) |
| 83 | $C_2$ | \( ( 1 + 198 T + p^{3} T^{2} )^{2} \) |
| 89 | $C_2^2$ | \( 1 - 873 T + 57160 T^{2} - 873 p^{3} T^{3} + p^{6} T^{4} \) |
| 97 | $C_2$ | \( ( 1 - 905 T + p^{3} T^{2} )^{2} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
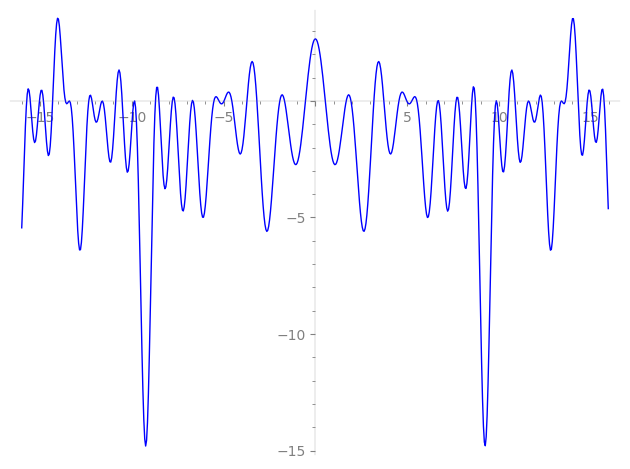
Imaginary part of the first few zeros on the critical line
−11.61595939956977917325381388217, −10.87663733857912810385549378940, −10.52347350809177073023003311604, −9.870614646406295478541701193121, −9.845772962812683512682944786070, −8.711027588200759454845834261384, −8.521929932245113448562572945076, −7.79128799611789623869127202294, −7.66467488021312200809117389385, −6.71275323890287446997463148733, −6.66060692510583233367211161893, −5.52728483315971359369703755432, −5.25160728937015250239526523957, −4.97808557586957136245218402540, −4.55205834926261843685614157964, −3.72990868445812782467973365925, −3.18671255893753030092555923343, −1.93870165713968558956903242917, −1.68020255793729217179742707131, −0.54077370024009379882716767394,
0.54077370024009379882716767394, 1.68020255793729217179742707131, 1.93870165713968558956903242917, 3.18671255893753030092555923343, 3.72990868445812782467973365925, 4.55205834926261843685614157964, 4.97808557586957136245218402540, 5.25160728937015250239526523957, 5.52728483315971359369703755432, 6.66060692510583233367211161893, 6.71275323890287446997463148733, 7.66467488021312200809117389385, 7.79128799611789623869127202294, 8.521929932245113448562572945076, 8.711027588200759454845834261384, 9.845772962812683512682944786070, 9.870614646406295478541701193121, 10.52347350809177073023003311604, 10.87663733857912810385549378940, 11.61595939956977917325381388217