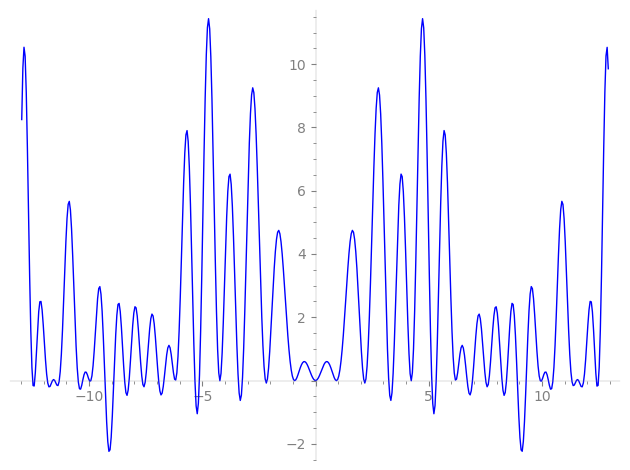
| L(s) = 1 | − 4·2-s − 6·3-s + 12·4-s − 13·5-s + 24·6-s − 17·7-s − 32·8-s + 27·9-s + 52·10-s + 14·11-s − 72·12-s − 19·13-s + 68·14-s + 78·15-s + 80·16-s − 12·17-s − 108·18-s − 156·20-s + 102·21-s − 56·22-s − 54·23-s + 192·24-s − 92·25-s + 76·26-s − 108·27-s − 204·28-s + 130·29-s + ⋯ |
| L(s) = 1 | − 1.41·2-s − 1.15·3-s + 3/2·4-s − 1.16·5-s + 1.63·6-s − 0.917·7-s − 1.41·8-s + 9-s + 1.64·10-s + 0.383·11-s − 1.73·12-s − 0.405·13-s + 1.29·14-s + 1.34·15-s + 5/4·16-s − 0.171·17-s − 1.41·18-s − 1.74·20-s + 1.05·21-s − 0.542·22-s − 0.489·23-s + 1.63·24-s − 0.735·25-s + 0.573·26-s − 0.769·27-s − 1.37·28-s + 0.832·29-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 4691556 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(4-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 4691556 ^{s/2} \, \Gamma_{\C}(s+3/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(2)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{5}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_1$ | \( ( 1 + p T )^{2} \) |
| 3 | $C_1$ | \( ( 1 + p T )^{2} \) |
| 19 | | \( 1 \) |
| good | 5 | $D_{4}$ | \( 1 + 13 T + 261 T^{2} + 13 p^{3} T^{3} + p^{6} T^{4} \) |
| 7 | $D_{4}$ | \( 1 + 17 T + 697 T^{2} + 17 p^{3} T^{3} + p^{6} T^{4} \) |
| 11 | $D_{4}$ | \( 1 - 14 T + 2631 T^{2} - 14 p^{3} T^{3} + p^{6} T^{4} \) |
| 13 | $D_{4}$ | \( 1 + 19 T + 4453 T^{2} + 19 p^{3} T^{3} + p^{6} T^{4} \) |
| 17 | $D_{4}$ | \( 1 + 12 T + 8417 T^{2} + 12 p^{3} T^{3} + p^{6} T^{4} \) |
| 23 | $D_{4}$ | \( 1 + 54 T + 24743 T^{2} + 54 p^{3} T^{3} + p^{6} T^{4} \) |
| 29 | $D_{4}$ | \( 1 - 130 T + 43758 T^{2} - 130 p^{3} T^{3} + p^{6} T^{4} \) |
| 31 | $D_{4}$ | \( 1 - 239 T + 41461 T^{2} - 239 p^{3} T^{3} + p^{6} T^{4} \) |
| 37 | $D_{4}$ | \( 1 - 4 p T + 74782 T^{2} - 4 p^{4} T^{3} + p^{6} T^{4} \) |
| 41 | $D_{4}$ | \( 1 + 331 T + 158201 T^{2} + 331 p^{3} T^{3} + p^{6} T^{4} \) |
| 43 | $D_{4}$ | \( 1 + 224 T + 160513 T^{2} + 224 p^{3} T^{3} + p^{6} T^{4} \) |
| 47 | $D_{4}$ | \( 1 - 333 T + 234917 T^{2} - 333 p^{3} T^{3} + p^{6} T^{4} \) |
| 53 | $D_{4}$ | \( 1 - 766 T + 306663 T^{2} - 766 p^{3} T^{3} + p^{6} T^{4} \) |
| 59 | $D_{4}$ | \( 1 - 460 T + 238938 T^{2} - 460 p^{3} T^{3} + p^{6} T^{4} \) |
| 61 | $D_{4}$ | \( 1 - 494 T + 436846 T^{2} - 494 p^{3} T^{3} + p^{6} T^{4} \) |
| 67 | $D_{4}$ | \( 1 - 133 T + 585147 T^{2} - 133 p^{3} T^{3} + p^{6} T^{4} \) |
| 71 | $D_{4}$ | \( 1 - 459 T + 693461 T^{2} - 459 p^{3} T^{3} + p^{6} T^{4} \) |
| 73 | $D_{4}$ | \( 1 - 396 T + 810393 T^{2} - 396 p^{3} T^{3} + p^{6} T^{4} \) |
| 79 | $D_{4}$ | \( 1 + 1000 T + 1157953 T^{2} + 1000 p^{3} T^{3} + p^{6} T^{4} \) |
| 83 | $D_{4}$ | \( 1 + 74 T + 1088763 T^{2} + 74 p^{3} T^{3} + p^{6} T^{4} \) |
| 89 | $D_{4}$ | \( 1 - 1180 T + 1585058 T^{2} - 1180 p^{3} T^{3} + p^{6} T^{4} \) |
| 97 | $D_{4}$ | \( 1 - 1938 T + 2745702 T^{2} - 1938 p^{3} T^{3} + p^{6} T^{4} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−8.430410264685719323933535863143, −8.233637849477821968614910306664, −7.65240212465732974196272479216, −7.51380225306798030448630884394, −6.92900960178569634208257131245, −6.69390117222560602127687952688, −6.19661364266334820923270181717, −6.19009496234630594361169576298, −5.32611046629390077947355774805, −5.13241117539274836311916726114, −4.23278744789764541215029951358, −4.21581326351207350952939263823, −3.40998004474691936595604678536, −3.23134069995633458518212389062, −2.21440901149163738246885046366, −2.13544963586915157016738093180, −0.939793968710059007423980471979, −0.903681331993177709262374872484, 0, 0,
0.903681331993177709262374872484, 0.939793968710059007423980471979, 2.13544963586915157016738093180, 2.21440901149163738246885046366, 3.23134069995633458518212389062, 3.40998004474691936595604678536, 4.21581326351207350952939263823, 4.23278744789764541215029951358, 5.13241117539274836311916726114, 5.32611046629390077947355774805, 6.19009496234630594361169576298, 6.19661364266334820923270181717, 6.69390117222560602127687952688, 6.92900960178569634208257131245, 7.51380225306798030448630884394, 7.65240212465732974196272479216, 8.233637849477821968614910306664, 8.430410264685719323933535863143