| L(s) = 1 | + 3-s + 9-s − 4·11-s + 4·13-s + 4·19-s + 27-s − 2·29-s − 8·31-s − 4·33-s − 6·37-s + 4·39-s − 4·43-s − 8·47-s − 10·53-s + 4·57-s + 4·59-s + 4·61-s − 4·67-s − 8·71-s + 16·73-s + 8·79-s + 81-s + 12·83-s − 2·87-s + 8·89-s − 8·93-s − 8·97-s + ⋯ |
| L(s) = 1 | + 0.577·3-s + 1/3·9-s − 1.20·11-s + 1.10·13-s + 0.917·19-s + 0.192·27-s − 0.371·29-s − 1.43·31-s − 0.696·33-s − 0.986·37-s + 0.640·39-s − 0.609·43-s − 1.16·47-s − 1.37·53-s + 0.529·57-s + 0.520·59-s + 0.512·61-s − 0.488·67-s − 0.949·71-s + 1.87·73-s + 0.900·79-s + 1/9·81-s + 1.31·83-s − 0.214·87-s + 0.847·89-s − 0.829·93-s − 0.812·97-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 235200 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 235200 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(2.199719623\) |
| \(L(\frac12)\) |
\(\approx\) |
\(2.199719623\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 2 | \( 1 \) | |
| 3 | \( 1 - T \) | |
| 5 | \( 1 \) | |
| 7 | \( 1 \) | |
| good | 11 | \( 1 + 4 T + p T^{2} \) | 1.11.e |
| 13 | \( 1 - 4 T + p T^{2} \) | 1.13.ae |
| 17 | \( 1 + p T^{2} \) | 1.17.a |
| 19 | \( 1 - 4 T + p T^{2} \) | 1.19.ae |
| 23 | \( 1 + p T^{2} \) | 1.23.a |
| 29 | \( 1 + 2 T + p T^{2} \) | 1.29.c |
| 31 | \( 1 + 8 T + p T^{2} \) | 1.31.i |
| 37 | \( 1 + 6 T + p T^{2} \) | 1.37.g |
| 41 | \( 1 + p T^{2} \) | 1.41.a |
| 43 | \( 1 + 4 T + p T^{2} \) | 1.43.e |
| 47 | \( 1 + 8 T + p T^{2} \) | 1.47.i |
| 53 | \( 1 + 10 T + p T^{2} \) | 1.53.k |
| 59 | \( 1 - 4 T + p T^{2} \) | 1.59.ae |
| 61 | \( 1 - 4 T + p T^{2} \) | 1.61.ae |
| 67 | \( 1 + 4 T + p T^{2} \) | 1.67.e |
| 71 | \( 1 + 8 T + p T^{2} \) | 1.71.i |
| 73 | \( 1 - 16 T + p T^{2} \) | 1.73.aq |
| 79 | \( 1 - 8 T + p T^{2} \) | 1.79.ai |
| 83 | \( 1 - 12 T + p T^{2} \) | 1.83.am |
| 89 | \( 1 - 8 T + p T^{2} \) | 1.89.ai |
| 97 | \( 1 + 8 T + p T^{2} \) | 1.97.i |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
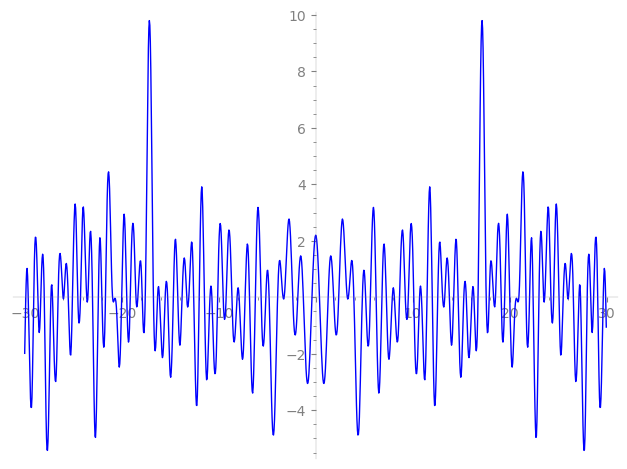
Imaginary part of the first few zeros on the critical line
−13.07071018594121, −12.57336786914599, −12.01237372631169, −11.47435516560084, −10.90887628031934, −10.70309165275537, −10.10863338783498, −9.541930227758330, −9.233890022461802, −8.641314010017914, −8.111406315775246, −7.889343523944694, −7.277058109798474, −6.821371614488950, −6.225216917694168, −5.634121978695931, −5.146272167221068, −4.802507356841845, −3.933017303642098, −3.375625706047872, −3.253152929113572, −2.370434208029738, −1.845204830783477, −1.278549555881314, −0.3876917263098326,
0.3876917263098326, 1.278549555881314, 1.845204830783477, 2.370434208029738, 3.253152929113572, 3.375625706047872, 3.933017303642098, 4.802507356841845, 5.146272167221068, 5.634121978695931, 6.225216917694168, 6.821371614488950, 7.277058109798474, 7.889343523944694, 8.111406315775246, 8.641314010017914, 9.233890022461802, 9.541930227758330, 10.10863338783498, 10.70309165275537, 10.90887628031934, 11.47435516560084, 12.01237372631169, 12.57336786914599, 13.07071018594121