| L(s) = 1 | − 24·2-s + 252·3-s − 1.47e3·4-s + 4.83e3·5-s − 6.04e3·6-s − 1.67e4·7-s + 8.44e4·8-s − 1.13e5·9-s − 1.15e5·10-s + 5.34e5·11-s − 3.70e5·12-s − 5.77e5·13-s + 4.01e5·14-s + 1.21e6·15-s + 9.87e5·16-s − 6.90e6·17-s + 2.72e6·18-s + 1.06e7·19-s − 7.10e6·20-s − 4.21e6·21-s − 1.28e7·22-s + 1.86e7·23-s + 2.12e7·24-s − 2.54e7·25-s + 1.38e7·26-s − 7.32e7·27-s + 2.46e7·28-s + ⋯ |
| L(s) = 1 | − 0.530·2-s + 0.598·3-s − 0.718·4-s + 0.691·5-s − 0.317·6-s − 0.376·7-s + 0.911·8-s − 0.641·9-s − 0.366·10-s + 1.00·11-s − 0.430·12-s − 0.431·13-s + 0.199·14-s + 0.413·15-s + 0.235·16-s − 1.17·17-s + 0.340·18-s + 0.987·19-s − 0.496·20-s − 0.225·21-s − 0.530·22-s + 0.603·23-s + 0.545·24-s − 0.522·25-s + 0.228·26-s − 0.982·27-s + 0.270·28-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\Gamma_{\C}(s) \, L(s)\cr=\mathstrut & \,\Lambda(12-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\Gamma_{\C}(s+11/2) \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(6)\) |
\(\approx\) |
\(0.7921228386\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.7921228386\) |
| \(L(\frac{13}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ |
|---|
| good | 2 | \( 1 + 3 p^{3} T + p^{11} T^{2} \) |
| 3 | \( 1 - 28 p^{2} T + p^{11} T^{2} \) |
| 5 | \( 1 - 966 p T + p^{11} T^{2} \) |
| 7 | \( 1 + 2392 p T + p^{11} T^{2} \) |
| 11 | \( 1 - 534612 T + p^{11} T^{2} \) |
| 13 | \( 1 + 577738 T + p^{11} T^{2} \) |
| 17 | \( 1 + 6905934 T + p^{11} T^{2} \) |
| 19 | \( 1 - 10661420 T + p^{11} T^{2} \) |
| 23 | \( 1 - 18643272 T + p^{11} T^{2} \) |
| 29 | \( 1 - 128406630 T + p^{11} T^{2} \) |
| 31 | \( 1 + 52843168 T + p^{11} T^{2} \) |
| 37 | \( 1 + 182213314 T + p^{11} T^{2} \) |
| 41 | \( 1 - 308120442 T + p^{11} T^{2} \) |
| 43 | \( 1 + 17125708 T + p^{11} T^{2} \) |
| 47 | \( 1 - 2687348496 T + p^{11} T^{2} \) |
| 53 | \( 1 + 1596055698 T + p^{11} T^{2} \) |
| 59 | \( 1 + 5189203740 T + p^{11} T^{2} \) |
| 61 | \( 1 - 6956478662 T + p^{11} T^{2} \) |
| 67 | \( 1 + 15481826884 T + p^{11} T^{2} \) |
| 71 | \( 1 - 9791485272 T + p^{11} T^{2} \) |
| 73 | \( 1 - 1463791322 T + p^{11} T^{2} \) |
| 79 | \( 1 - 38116845680 T + p^{11} T^{2} \) |
| 83 | \( 1 + 29335099668 T + p^{11} T^{2} \) |
| 89 | \( 1 + 24992917110 T + p^{11} T^{2} \) |
| 97 | \( 1 - 75013568546 T + p^{11} T^{2} \) |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−32.77487538223120744183045567331, −31.17820949836025906449218889077, −28.83168262418687544502196191298, −26.80439115835040303257574923358, −25.27463654811236535674532419313, −22.33610363720986727568267445924, −19.65651314195496100012728175632, −17.44277697823447331355152513713, −13.90754986139213440644668132877, −9.222379399921102522243767192743,
9.222379399921102522243767192743, 13.90754986139213440644668132877, 17.44277697823447331355152513713, 19.65651314195496100012728175632, 22.33610363720986727568267445924, 25.27463654811236535674532419313, 26.80439115835040303257574923358, 28.83168262418687544502196191298, 31.17820949836025906449218889077, 32.77487538223120744183045567331
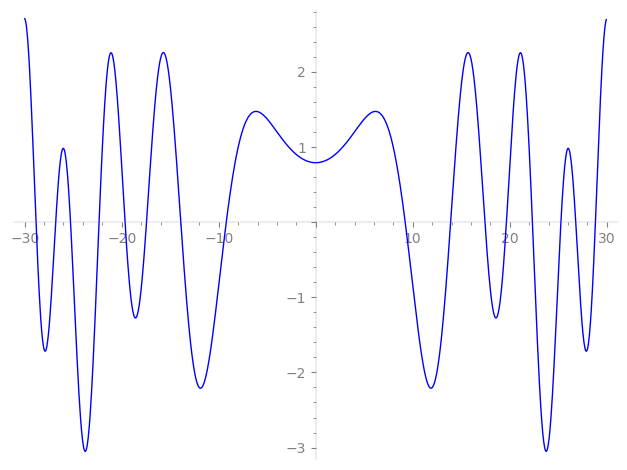
The first zero of this L-function, at height approximately 9.222, is the highest among primitive algebraic degree 2 L-functions.
